深入理解树状数组-京东云开发者社区

#### 树状数组

树状数组（BIT, Binary Indexed Tree）是简洁优美的数据结构，它能在很少的代码量下支持 **单点修改** 和 **区间查询**，我们先以 `a[] {1, 2, 3, 4, 5, 6}` 数组为例建立树状数组看一下树状数组的样子：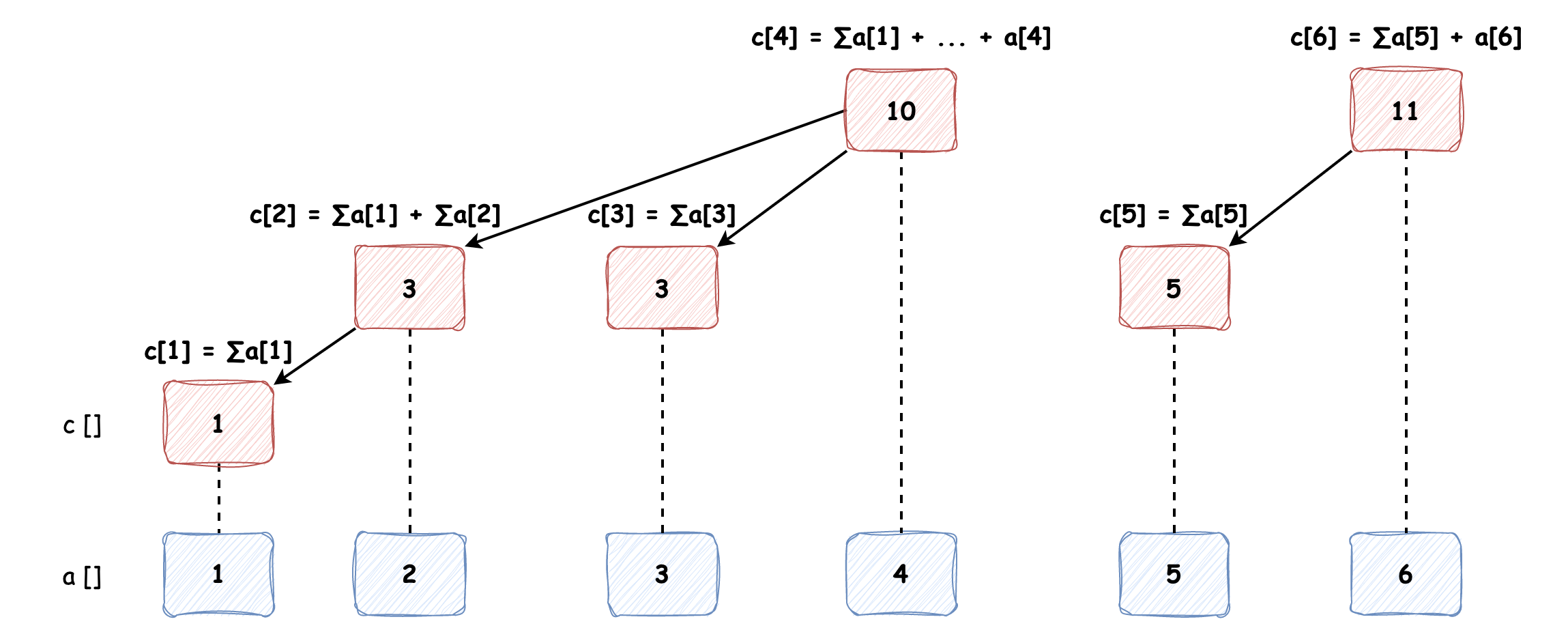

![树状数组.png](https://s3.cn-north-1.jdcloud-oss.com/shendengbucket1/2023-08-28-09-07xVoOEcOi82828q9mZ.png)

可以发现：不是所有节点都是连接在一起的，c\[1\], c\[2\], c\[3\], c\[4\] 和 c\[5\], c\[6\] 分别构成了两棵树；奇数索引位置的节点只管辖一个数组元素（我们例子中以 1 为起始索引）。那么这个树状数组是怎么计算和推导出来的呢？

#### 管辖的区间

树状数组的每个元素会管辖多少个数组元素？也就是说每个元素的区间长度是多少？我们从上图中已经知道了奇数的树状数组元素只管辖一个元素，区间为 c\[x\] = \[x, x\]，那么我们只需再研究下偶数元素管辖的区间长度即可。

* c\[y\] 所管辖的区间长度为 2k ，其中 k 为 y 的 2 进制表示中最低位 1 后面所有 0 的数量；c\[y\] 所管辖的区间为：\[y - 2k + 1, y\]

我们以 c\[4\] 为例，它管辖多少个元素呢？4 的 2 进制表示为 0100，最低位 1 后面 0 的数量为 2，即 k = 2，那么 2k = 22 = 4，所以它管辖的区间长度为 4，也就是 4 个数组元素，区间为 \[4 - 4 + 1, 4\] = \[1, 4\]。

#### 父节点是谁？

现在我们知道每个元素所管辖的区间范围了，那么我们怎么才能知道它的父节点是谁呢？就比如说我们现在得到了 c\[1\] 元素，我们想知道它的父节点，要怎么计算呢？

* c\[x\] 的父节点为 c\[x + lowbit(x)\]

怎么回事？其中的 **lowbit(x)** 是什么东西？其实它的值和 2k 一致，**其中 k 为 x 的 2 进制表示中最低位 1 后面所有 0 的数量**，熟悉不熟悉？这个 lowbit(x) 和我们上文中计算该元素所管辖区间长度的值一致！这不就简单了！

* lowbit(x) 的计算方法：lowbit(x) = x & -x
 
 我们以计算 c\[2\] 为例，lowbit(2) = 2 & -2，其中 2 的 2 进制表示为 0010，-2 的 2 进行表示为 1110，它的计算方法为将 2 的所有非符号位二进制全部取反后再加 1，即 1101 + 1 = 1110，执行 & 运算后结果为 0010，十进制表示为 2，与 21 值一致。lowbit 的计算用代码表示为：
 
 ```java
 int lowbit(int x) {
 return x & -x;
 }
 ```

我们以 c\[1\] 节点为例计算下它的父节点是谁，lowbit(1) = 1 & -1 = 0001 & 1111 = 0001 = 1，那么它的父节点为 c\[1 + 1\] = c\[2\]，与图上表示的一致。

---

现在我们已经知道如何通过计算来创建树状数组了， 接下来我们要看下它的应用。

#### 区间查询

区间查询我们先讨论计算前 N 项和的方法，比如我们现在要查询前 6 项和，我们来看下它查询的过程：

* 从 c\[6\] 开始找子节点，有 c\[6\] 管辖的区间为 \[5, 6\]，那么再往下找需要找 c\[4\]，它的区间为 \[1, 4\]，计算这两个节点的和即可。

那么从 c\[6\] 跳到 c\[4\] 是如何计算出来的呢？我们可以通过 c\[6\] 区间的下界减 1 来得到，转换成公式表示即为 x - lowbit(x) = 6 - 2 = 4，当它跳到 c\[4\] 时发现已经满足求和条件，不再向下跳而结束查找，而且我们可以通过计算 4 - lowbit(4) = 4 - 4 = 0 ，可以发现当 x - lowbit(x) = 0 时为结束查找的条件。我们用代码来表示为：

```java
    int query(int x) {
        int res = 0;
        for (int i = x; i > 0; i -= lowbit(i)) {
            res += c[i];
        }
        
        return res;
    }
```

那么我们计算区间 \[3, 6\] 的和该如何计算呢？我们从图中可以发现，先计算出\[1, 6\] 和 \[1, 2\] 的和，再使用前者减去后者即为所得，用代码表示为：

```java
    int query(int left, int right) {
        return query(right) - query(left - 1);
    }
```

#### 单点修改

如果我们要修改 a\[x\] 的值，我们仅需要修改所有管辖了 a\[x\] 的 c\[y\] 即可，而 a\[x\] 可能会被多个 c\[y\] 管辖，这些所有的 c\[y\] 节点该如何确定呢？我们可以回头再去看看前面的树状数组配图，比如我们要修改 a\[1\] 的值，那么我们需要修改 c\[1\], c\[2\] 和 c\[4\] ，能不能发现它是在不断的 **跳父节点** 修改？所以，**如果我们要修改数组中某个元素的值，树状数组的更新则是不断地更新父节点值**。好，我们直接上代码吧：

```java
    // 将 index 索引处的值更新为 num
    void update(int index, int num) {
        a[index] = num;
        add(index, num - a[index]);
    }

// 更新 c[index] 的值，变化差值为 val
 void add(int index, int val) {
 for (int i = index; i <= c.length; i += lowbit(i)) {
 c[i] += val;
 }
 }
```

#### 建树

好了，区间查询和单点修改我们都讲完了，但是从头到尾我们还没说过树状数组是怎么建立的呢。我们可以想一下，c 数组初始化时每个索引处的值都为 0，建树仅需要将 a 数组中所有值都在树状数组中执行单点修改即可：

```java
 public BinaryIndexedTree(int[] a) {
 this.a = a;
 this.c = new int[a.length + 1];
 
 for (int i = 0; i < a.length; i++) {
 add(i + 1, a[i]);
 }
 }
```

到这里我们基本上已经将树状数组讲解完毕了，它的全量代码如下：

```java
public class BinaryIndexedTree {

int[] a;

int[] c;

public BinaryIndexedTree(int[] a) {
        this.a = a;
        this.c = new int[a.length + 1];

for (int i = 0; i < a.length; i++) {
 add(i + 1, a[i]);
 }
 }

// 将 index 索引处的值更新为 num
    void update(int index, int num) {
        a[index] = num;
        add(index, num - a[index]);
    }

// 更新 c[index] 的值，变化差值为 val
 void add(int index, int val) {
 for (int i = index; i < c.length; i += lowbit(i)) {
 c[i] += val;
 }
 }

int query(int left, int right) {
        return query(right) - query(left - 1);
    }

// 查询前缀和的方法
    int query(int x) {
        int res = 0;
        for (int i = x; i > 0; i -= lowbit(i)) {
            res += c[i];
        }

return res;
    }

int lowbit(int x) {
        return x & -x;
    }
}
```

---

#### 巨人的肩膀

* [树状数组（简单介绍）](https://blog.csdn.net/qq_40941722/article/details/104406126)
    
* [负数的二进制表示方法（正数：原码、负数：补码）](https://www.cnblogs.com/andy-0212/p/10323502.html)
    
* [树状数组](https://oi-wiki.org/ds/fenwick/)
    
* [算法学习笔记(2) : 树状数组](https://zhuanlan.zhihu.com/p/93795692)
    
* [维基百科 - 树状数组](https://zh.wikipedia.org/zh-cn/%E6%A0%91%E7%8A%B6%E6%95%B0%E7%BB%84)
    
* [关于各类「区间和」问题如何选择解决方案（含模板）](https://leetcode.cn/problems/range-sum-query-mutable/solutions/632515/guan-yu-ge-lei-qu-jian-he-wen-ti-ru-he-x-41hv/)
    
* [算法学习笔记(19): 离散化](https://zhuanlan.zhihu.com/p/112497527)