差分隐私（Differential Privacy，DP）是密码学中的一种手段，可以提高从统计数据库进行数据查询的准确性，同时帮助最大限度减少识别其具体记录的机会。DP一般分为：CDP（Centralized Differential Privacy）、LDP（Local Differential Privacy）。

一、CDP

1.1 基本定义

只相差一个样本的两个数据集称为邻近数据集。给定，我们称一个随机算法M（把数据集映射为一个数）满足，只要它满足如下条件：对于任意的邻居数据集pair和任何可能的值域子集E，成立[1]。其中称为隐私预算。上式中，f(x)是确定性函数，Z是对f(x)添加的随机噪声。

接下来，我们给出近似差分隐私定义如下：。其中表示失败概率，我们以的概率获得的保护程度，以的概率不满足。稍后在介绍Gaussian时会用到此定义。

保护效果：查询者无法判断特定样本是否在一个数据集当中。

1.2 应用举例

假设f(x)是COUNT聚合函数，我们对COUNT结果追加Laplace扰动，相应公式为[2]：，则M(x)满足。其中s是f(x)的全局敏感度（稍后会介绍），是隐私预算，Laplace(S)代表均值为0，缩放系数为S的拉普拉斯分布采样。相应的系统架构如下：

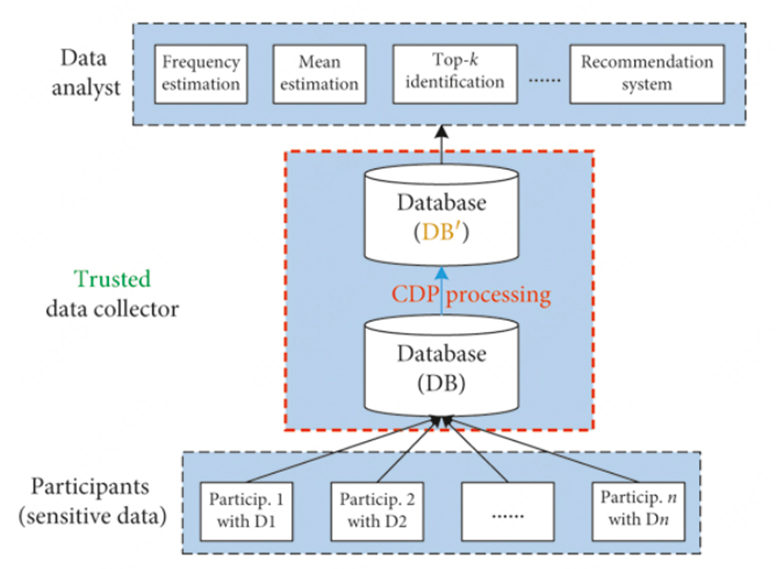
1.3 全局敏感度

给定一个将数据集映射为实数的函数f，f的全局敏感度定义如下：。从定义可知，全局敏感度和具体问询的全量数据集无关，对于任意邻近数据集x,x'上式都成立。对计数问询COUNT函数而言，其全局敏感度为1。

1.4 数据裁剪

COUNT函数的GS始终为1，但是SUM函数的GS就不好说了，因为这要看SUM作用于哪个属性列，如：年龄和收入应用SUM就有很大差异。如1.2所述，我们应用Laplace扰动机制时需要f(x)（此处为SUM）的有界全局敏感度，但SUM显然不容易做到，因此需要对待处理的列进行裁剪处理，以得到f(x)的有界全局敏感度。有两点需要特别注意：

在裁剪造成的信息损失与满足差分隐私所需要的噪声间进行trade off，一般裁剪后要尽可能保留100%的信息。
不能通过查看数据集来确定裁剪边界，这可能会泄露信息，同时也不满足差分隐私的定义。

那我们应该如何对属性列进行裁剪动作，一般有如下两个做法：

根据数据集先天满足的一些性质来确定裁剪办界。如人的年龄一般在0~125岁之间。
采用差分隐私问询估计选择的边界是否合理。先通过数据变换把属性列映射为非负值，然后将裁剪下界置0，逐渐增加上界，直至问询输出不变。

当对年龄求SUM时，可将裁剪上界从0~100逐渐变化，并对每次问询使用Laplace机制保证查询过程满足差分隐私。我们进行100次的问询。根据串行组合性（稍后再谈DP的组合问题），整个100次查询的总隐私消耗量。

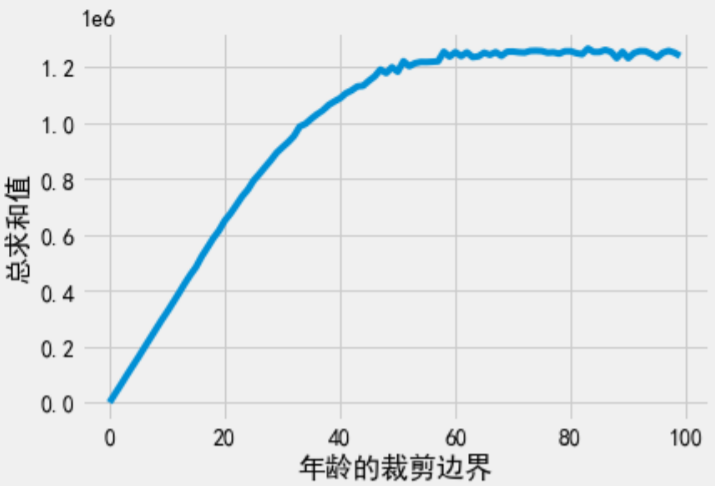
1.5 向量值函数及其敏感度

前文我们讨论的f(x)都是实值函数（将数据集映射为一个实数），接下来我们考虑向量值函数（将数据集映射为一个实数向量）。我们先给出L1和L2范数的定义（给定长度为k的向量V）：

L1范数：
L2范数：

同一向量的L2范数总是小于或等于L1范数。将下来我们给出向量值函数的L1敏感度和L2敏感度。

向量值函数f(x)的L1敏感度：，此敏感度等于向量各个元素敏感度之和。
向量值函数f(x)的L2敏感度：，此敏感度等于向量各个元素敏感度的平方和，再求算术平方根。

注：Laplace和Gaussian机制都可以扩展至向量值函数的情形。同一对象的L2敏感度要显著低于L1敏感度。

1.6 Laplace机制

如应用1.2所示，Laplace可以满足。Laplace(S)表示均值为0，缩放系数为S的拉普拉斯分布采样。S的值越小，则Laplace曲线越陡峭。下图给出当S取1、1.2时相应的pdf曲线。

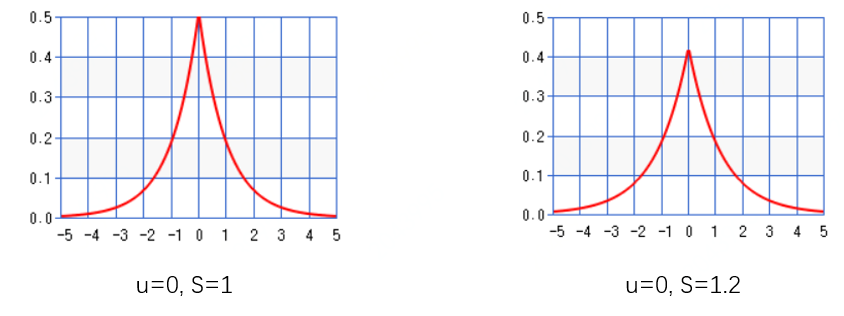
1.7 Gaussian机制

Gaussian机制无法满足，但可以满足。对于一个返回数值的函数f(x)，应用下述定义的高斯机制就可以得到满足的F(x)：。其中s是f(x)的敏感度，表示均值为0，方差为的高斯正态分布采样结果。下图给出标准差为1、1.1时的Gaussian pdf曲线。

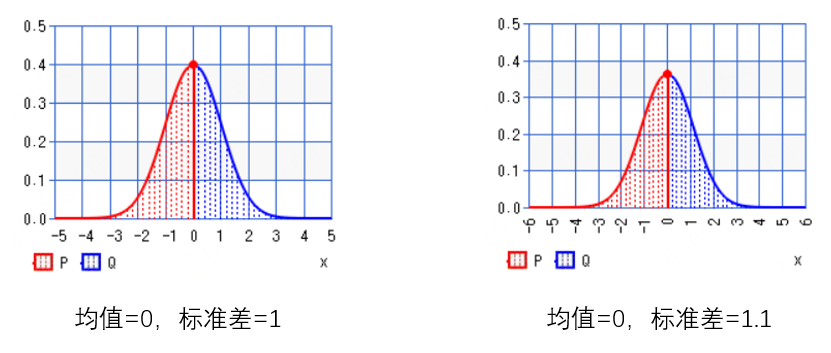
1.8 Laplace vs Gaussian

向量值Laplace机制需要使用L1敏感度，而向量值Gaussian机制L1和L2敏感度都可以使用。在L2敏感度远低于L1敏感度的场景下，Gaussian机制添加的噪声要小得多。向量值Laplace和Gaussian的发布规则为：

向量Laplace机制发布的是，其中是独立同分布的Laplace噪声，噪声尺度为，其中s是f的L1敏感度。
向量Gaussian机制发布的是，其中是独立同分布的Gaussian噪声，且，其中s是f的L2敏感度。

1.9 指数机制

前述Laplace和Gaussian机制的回复都是数值型的，只需要直接在回复的数值结果上添加噪声即可。如果我们想从一个备选回复集合中选出最佳结果，同时又保证回复过程满足差分隐私，那应该怎么办呢？一种可行的方法是使用指数机制。首先，定义一个备选回复集合；然后，再定义评分函数，评分函数输出备选集合中每个回复的分数；分数最高的回复就是最大回复。指数机制通过返回分数近似最大的回复来实现差分隐私保护。指数机制满足：

选择一个备选回复集合R
指定一个全局敏感度为的评分函数u
指数机制输出回复，每个回复的输出概率与成正比

可以看到，与Laplace机制相比，指数机制的不同之处在于总会输出集合R中的一个元素。

如下我们给出有限集合的指数机制代码样例

options = adult['Marital Status'].unique()
def score(data, option):
    return data.value_counts()[option]/1000

def exponential(x, R, u, sensitivity, epsilon):
    scores = [u(x, r) for r in R]     # 计 算R中 每 个 回 复 的 分 数 
    probabilities = [np.exp(epsilon * score / (2 * sensitivity)) for score in scores]   # 根 据 分 数 计 算 每 个 回 复 的 输 出 概 率  
    probabilities = probabilities / np.linalg.norm(probabilities, ord=1)  # 对 概 率 进 行 归 一 化 处 理 ， 使 概 率 和 等 于1
    return np.random.choice(R, 1, p=probabilities)[0]     # 根 据 概 率 分 布 选 择 回 复 结 果
exponential(adult['Marital Status'], options, score, 1, 1)   # 输出 'Married-civ-spouse'

r = [exponential(adult['Marital Status'], options, score, 1, 1) for i in range(200)]
pd.Series(r).value_counts() # output: Married-civ-spouse 185     Never-married 15

报告噪声最大值

当R为有限集合时，指数机制基本思想是从集合中选择元素的过程满足差分隐私。可以用拉普拉斯机制对此思想进行朴素实现：

对于每个，计算噪声分数
输出噪声分数最大的元素

评分函数u在x上的敏感度为，所以步骤1中的每次问询都满足。如果集合R包含n个元素，计算整个集合的噪声分数并将其全部发布，此过程满足。根据后处理性，上述步骤2的输出也满足，因为前述已发布所有带噪分数。

指数机制仅发布最大噪声分数所对应的元素，但不发布最大噪声分数本身，也不会发布其他元素的噪声分数。同样地，上述算法（step1+step2，也被称为报告噪声最大值）也只发布了最大噪声分数所对应的回复，所以无论集合R包含多少备选回复，此算法都满足[3]。

def report_noisy_max(x, R, u, sensitivity, epsilon):
    scores = [u(x, r) for r in R]     # 计算R中每个回复的分数
    noisy_scores = [laplace_mech(score, sensitivity, epsilon) for score in scores]    # 为每个分数增加噪声
    max_idx = np.argmax(noisy_scores)   # 找到最大分数对应的回复索引号
    return R[max_idx]   # 返回此索引号对应的回复
report_noisy_max(adult['Marital Status'], options, score, 1, 1)   # 输出'Married-civ-spouse'

r = [report_noisy_max(adult['Marital Status'], options, score, 1, 1) for i in range(200)]
pd.Series(r).value_counts()  #output: Married-civ-spouse 196    Never-married 4

指数机制非常具有普适性，只要精心设计评分函数u，可以用指数机制重定义任何。指数机制定义的差分隐私机制一般比较难实现，指数机制通常用于证明理论下界。在实际中，一般会使用其他算法来复现指数机制（如前述报告噪声最大值）。当R为有限集合时，可以用报告噪声最大值机制代替指数机制。当R为无限集合时，对集合中每个元素对应的分数增加Laplace噪声很困难，因此当R为无限集合时就不得不使用指数机制。无限集合下指数机制定义概率密度比较容易，但对应的高效采样算法很难设计。因此在很多论文中会用指数机制证明存在某些特定性质的差分隐私算法。

1.10 组合性与后处理性

在相同的输入数据上发布多次差分隐私机制保护下的结果时，串行组合性给出了总隐私消耗量。具体内容为：

如果满足
如果满足
则发布两个结果的机制满足

并行组合性将数据集拆分为互不相交的子数据块，在子数据块上分别应用相应的差分隐私机制。具体内容为（以为例）：

如果满足
将数据集X切分为互不相交的子数据块
则发布所有结果的机制的机制满足

后处理性指不可能通过某种方式对差分隐私保护下的数据进行后处理，来降低差分隐私的隐私保护程度。具体内容为：

如果满足
则对于任意（确定或随机）函数g，也满足

二、LDP

2.1 LDP基本定义

一个随机算法A满足，当时，对，下式成立：

，其中表示A的值域。当时，算法A称为纯粹本地差分隐私，简记为；当时，算法A称为近似本地差分隐私，简记为[4]。

保护效果：其他角色（客户端或中心服务器）无法区分客户端A中的不同样本。相应的算法架构如下：

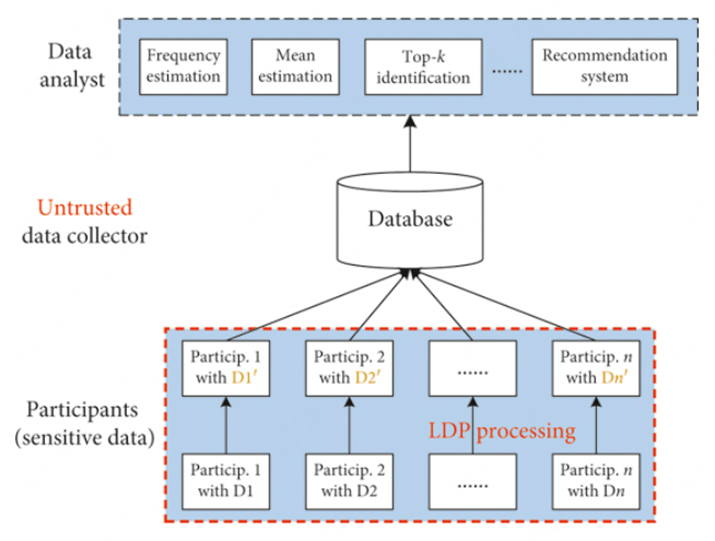
2.2 LDP经典算法

基于随机响应

二值离散变量：W-RR，举例见2.3
多值离散变量（二进制编码）：RAPPOR、SHist
多值离散变量（改进概率分布）：K-RR、GRR、ORR
处理多维数值变量：pMeanEst、Harmony-mean(采样)

基于信息论的干扰机制

Compression
Distortion

2.3 LDP举例-随机应答

有n个用户，假设X病患者的真实比例为，我们希望对这个比例进行统计。于是我们发起一个敏感问题：“你是否为X病患者？”，每个用户的答案是yes or no。出于隐私性考虑，用户可能不会给出正确答案[5]。

我们可以对每位用户的回答加一些数据扰动。比如：用户正确回答的概率为p，错误回答概率为(1-p)。这样就不会准确知道每位用户的真实答案，相当于保护了用户隐私。按此规则我们统计回答yes与no的用户占比。

扰动性统计

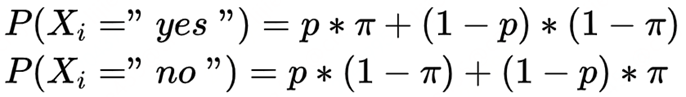
校正过程

上述统计并非真实比例的无偏估计，因此需要校正。构建如下似然函数（n1代表回答yes人数，n-n1为回答no的人数）：

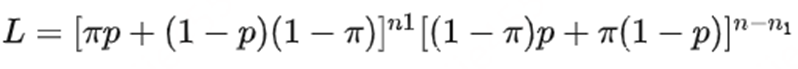
得到极大似然估计为（无偏估计）：

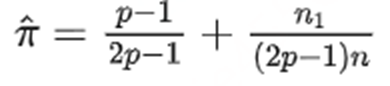
要满足，则；如果固定隐私预算的话，。

实例验证

共有n=50人（已知），其中10人为阳（未知），40人为阴（未知）。每人以p=0.8概率真实上报（已知）。则统计结果如下：

阳性统计值n1=10*0.8+40*0.2=16
阴性统计值=40*0.8+10*0.2=34

修正的阳性值=50*(-1/3)+160/6=10

DP在机器学习领域的应用、基于Gaussian机制实现LDP的原理请听下回分享。

参考资料

1.Balle B, Wang Y X. Improving the gaussian mechanism for differential privacy: Analytical calibration and optimal denoising[C]//International Conference on Machine Learning. PMLR, 2018: 394-403.

2. https://programming-dp.com/

3.Cynthia Dwork, Aaron Roth, and others. The algorithmic foundations of differential privacy. Foundations and
Trends® in Theoretical Computer Science, 9(3–4):211–407, 2014.

4.Xiong X, Liu S, Li D, et al. A comprehensive survey on local differential privacy[J]. Security and Communication Networks, 2020, 2020: 1-29.

5.LDP随机响应技术举例： https://zhuanlan.zhihu.com/p/472032115

【差分隐私】1-基本原理与入门级应用