本地图像描述符：现代方法

——
作者：Bin Fan，Zhenhua Wang，Fuchao Wu

有关该系列的更多信息，请访问*http://www.springer.com/series/10028*

目录

1 引言. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 1
参考文献 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3
2 经典的本地描述符. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5
2.1 尺度不变特征变换 (SIFT) . . . . . . . . . . . . . . . . . . 5
2.1.1 SIFT中的比例尺空间表示. . . . . . . . . . . . . . . . . 6
2.1.2 关键点检测 . . . . . . . . . . . . . . . . . . . . . . . . . . . . 7
2.1.3 功能描述 . . . . . . . . . . . . . . . . . . . . . . . . . . . . 9
2.2 加快了鲁棒性 (SURF) . . . . . . . . . . . . . . . . . . . . . 11
2.2.1 积分图像. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 11
2.2.2 SURF中的尺度空间表示 . . . . . . . . . . . . . . . . 11
2.2.3 尺度不变兴趣点检测 . . . . . . . . . . . . . . 14
2.2.4 方向分配和描述符的构造 . . . . . 14
2.3 局部二元模式及其变异 . . . . . . . . . . . . . . . . . . . . . 16
参考文献 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 23
3 基于强度顺序的本地描述符. . . . . . . . . . . . . . . . . . . . . 25
3.1 序数和空间强度分布描述符 (OSID). . . . . 25
3.2 基于强度顺序的特征描述池化 . . . . . . . . . 26
3.2.1 基于几何的空间池分析 . . . . . 27
3.2.2 基于强度顺序的补丁分区. . . . . . . . . . . . . . . . 30
3.2.3 MROGH和MRRID描述符的构造 . . . . . . 31
3.3 用于特征描述的局部强度顺序模式 . . . . . . . . . . 33
3.3.1 LIOP描述符的构造 . . . . . . . . . . . . . . . . 34
3.4 基于强度阶的二进制描述符 . . . . . . . . . . . . . . . . . . . 34
3.4.1 次区域生成 . . . . . . . . . . . . . . . . . . . . . . . . . . 35
3.4.2 区域不变式和成对比较 . . . . . . . . . 37
3.4.3 学习好的二进制描述符 . . . . . . . . . . . . . . . . . . 39
3.4.4 使用多个支持区域. . . . . . . . . . . . . . . . . . . 40
3.4.5 级联过滤以加快匹配速度 . . . . . . . . . . . 40
参考文献 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 41
4 Burgeoning方法：二进制描述符. . . . . . . . . . . . . . . . . . . . 43
4.1简介：二进制健壮的独立基本特征. . . . . . . 43
4.2 ORB：定向的FAST和旋转的Brief. . . . . . . . . . . . . . . . . 44
4.2.1尺度不变FAST检测器. . . . . . . . . . . . . . . . . . . . 45
4.2.2强度中心的方向计算. . . . . . . . . 45
4.2.3学习良好的二进制特性. . . . . . . . . . . . . . . . . . . . 46
4.3 BRISK：二进制鲁棒和不变的可扩展关键点. . . . . . . 47
4.3.1关键点检测. . . . . . . . . . . . . . . . . . . . . . . . . . . . 47
4.3.2方向分配和关键点描述. . . . . . . 49
4.4 FREAK：快速视网膜关键点. . . . . . . . . . . . . . . . . . . . . . . . . 50
4.4.1描述符的构造. . . . . . . . . . . . . . . . . . . . . . . . . 50
4.4.2与FREAK的节奏匹配. . . . . . . . . . . . . . . . . . . 51
4.5 FRIF：快速鲁棒不变特征. . . . . . . . . . . . . . . . . . . . . . 52
4.5.1 FALoG检测器. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 52
4.5.2混合二进制描述符. . . . . . . . . . . . . . . . . . . . . . . . 53
4.6通过监督信息学习二进制描述符. . . . . . . . 54
4.6.1从原始映像补丁开始. . . . . . . . . . . . . . . . . . . . . . . . . 55
4.6.2来自中间表示. . . . . . . . . . . . . . . . 62
参考文献. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 65岁
5视觉应用程序. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 69
5.1运动和3D重建的结构. . . . . . . . . . . . . . . 69
5.2对象识别. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 74
5.3基于内容的图像检索. . . . . . . . . . . . . . . . . . . . . . . . . 77
5.4同时定位和映射(SLAM). . . . . . . . . . . . 81
参考文献. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 86
6资源和未来工作. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 89
6.1数据集和评估协议. . . . . . . . . . . . . . . . . . . . . . . . 89
6.1.1图像匹配基准. . . . . . . . . . . . . . . . . . . 89
6.1.2对象识别基准. . . . . . . . . . . . . . . . . 92
6.1.3图像检索基准. . . . . . . . . . . . . . . . . . . 93
6.2结论和今后的工作. . . . . . . . . . . . . . . . . . . . 95
参考文献. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 97

第2章古典本地描述符

**摘要：**经典的局部描述符是指多年前提出的，但对局部图像描述及其相关应用的发展产生了深远的影响。尺度不变特征变换(SIFT)和加速鲁棒特征(SURF)是计算机视觉中两个广泛使用的描述符。特别是对于SIFT，它是从对象识别，图像检索到运动构造等各种应用程序的极受欢迎解决方案。而对于SURF，对于需要快速或接近实时的应用程序，它是首选。图像匹配，直到最近的二进制描述符蓬勃发展。另一个经典的局部特征是1990年代提出的局部二进制模式(LBP)。与许多变体一起，LBP在纹理分类和许多与面部相关的任务(例如，面部识别，面部检测和面部表情识别)中无处不在。由于它们的受欢迎程度，我们选择在本章中详细介绍它们。

关键词 SIFT SURF LBP标度空间表示浮点型描述符

2.1尺度不变特征变换(SIFT)

尺度不变特征变换(SIFT)[9]是最成功的局部描述符之一，已广泛用于各种视觉任务，例如图像分类，图像检索，图像配准，姿势估计等。 SIFT基本上包括特征检测和特征描述。根据上下文和应用，有时SIFT仅指代其用于特征描述的方法，即SIFT特征描述符。为了清楚起见，术语“ SIFT关键点”通常用于指示其检测到的功能。

一般而言，SIFT是尺度不变的方法，同时保持了许多其他图像变换的稳健性，包括平面内旋转，较小的视角改变(由相机的平面外旋转引起)，图像模糊，照明和噪声。 SIFT特征检测器可实现尺度不变性及其对图像旋转的鲁棒性，它可以检测关键点及其尺度和参考方向。而通过构造SIFT描述符获得对其他转换的鲁棒性。

2.1.1 SIFT中的比例尺空间表示

为了实现尺度不变性，SIFT在高斯尺度空间上运行以检测关键点并构造其局部描述符。输入图像的高斯比例空间定义为通过将输入图像与逐渐增加的高斯方差卷积而获得的一系列图像。给定输入图像I(x，y)，其高斯卷积图像可以表示为：

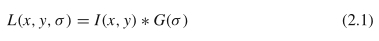
其中G(σ)表示标准差为σ的高斯滤波器。因此，一组卷积图像{L(x，y，σi)，i = 1、2，…，n}用来表示图像I的高斯尺度空间。在实施SIFT时，σ增加了一个常数k，即σi+1 =kσi。

为了检测对缩放变化具有鲁棒性且具有高重复性的关键点，SIFT将DoG(高斯差分)尺度空间中的极值用作初始关键点，然后进行一些改进和调整以确定最终关键点(将在下一节中进行介绍)。为此，通过减去相邻的图像比例，在高斯比例空间的基础上构建DoG比例空间：

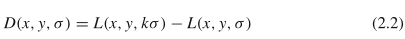
高斯卷积的计算时间与图像的大小以及使用的高斯核的大小呈正相关。因此，为了提高效率，通过将L(σi)与σ’i+1 =√(σi+12 - σi2)进行卷积来计算L(σi+1)，而不是直接对σi+1进行卷积。另一方面，SIFT还使用基于八度的结构表示比例空间。更具体地，将标度空间中的图像划分为八度音程，每个八度度使σ加倍，即标度。在每个八度音程中，它将刻度空间进一步划分为s层，因此，ks = 2时，k = 21/s。正如我们稍后将描述的，SIFT沿着三个维度在DoG刻度空间中搜索极值以进行关键点检测。因此，它需要s + 2个DoG图像来覆盖一个完整的八度。如图2.1所示，两个附加层用于第一层和最后一层中的关键点检测。因此，需要s + 3高斯模糊图像来生成这些s + 2 DoG图像。在处理了一个八度之后，该八度中的第(s + 1)个图像将进行2倍的下采样，以在下一个八度中生成第一个图像。这样，整个八度音阶将覆盖一组以恒定因子增加的音阶，如图2.1所示。

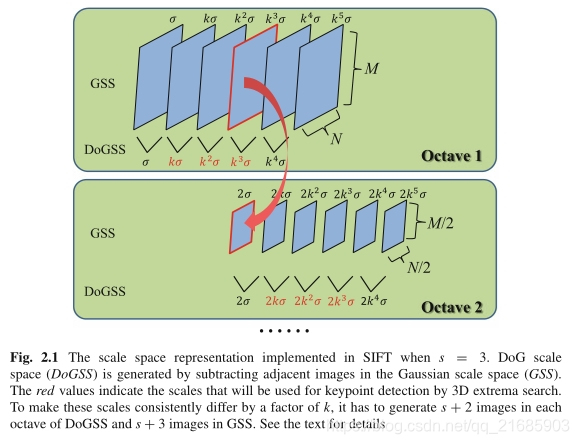
图2.1当s = 3时，在SIFT中实现的标尺空间表示。DoG标尺空间(DoGSS)是通过减去高斯标尺空间(GSS)中的相邻图像而生成的。 红色值表示将用于3D极值搜索的关键点检测的比例。 为了使这些比例尺始终相差k倍，必须在DoGSS的每个八度音程中生成s + 2图像，在GSS中生成s + 3图像。 详情请参阅文本

根据一些实验，Lowe建议将σ设置为1.6 [9]。同时，为了获得更稳定的关键点，他还建议将原始图像加倍2倍，并用它来构建比例尺空间的第一个八度。

2.1.2关键点检测

为了检测尺度不变的关键点，SIFT首先通过将每个像素与其当前层中的8个邻居以及上层和下层中的18个邻居进行比较来搜索D(x，y，σ)的局部最大值和最小值。然后，使用非最大抑制来滤除那些足够接近但不稳定的局部极值，从而获得离散位置和某些级别的预定义比例尺上的一组点。下一步是估计准确的位置(最多子像素)和比例。同时，重要的是要删除一些对比度较低的关键点以及沿边缘定位较差的关键点，因为这两种情况都会导致不稳定的关键点。

关键点X0 =(x，y，σ)的精确定位是通过在X0的局部区域周围拟合3D二次函数并取其极值的内插位置而获得的。为此，我们首先必须将比例响应函数的原点，即DoG响应，移至X0。然后，将泰勒展开式应用于位移的D(x，y，σ)：

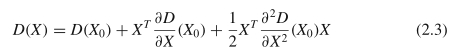
要获得D(X)的极值，我们可以计算D(X)的导数并将其设置为零。这样，我们得到以下方程式：

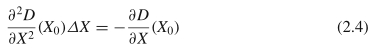
ΔX是极端点到原始点X0的偏移量，因此精炼的关键点位于X = X0 +ΔX处。值得注意的是，如果偏移ΔX在任何维度上均大于0.5，则表示极值位于更靠近X0的相邻点的位置。在这种情况下，将X0更改为该相邻点，并重复上述获取偏移的过程，直到偏移中的所有尺寸均小于0.5。

将X = X0 +ΔX代入公式(2.3)，我们可以获得其DoG值：

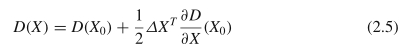
| D(X)|的极值小于0.03(假定像素值在[0,1]范围内)的像素由于对比度低(对噪声敏感)而被丢弃。

由于DoG函数将在边缘产生强烈的响应，因此这种极值对噪声不稳定，通常具有较大的定位误差。同时，沿边缘定位的点通常具有较不明显的局部外观，这将使得为它们提取区分描述符变得困难。由于这些原因，必须将它们丢弃。

除了在DoG尺度空间中的极端响应外，这些点在边缘的主曲率也大，而在垂线方向的主曲率则小。这两个曲率与Hessian矩阵H的特征值成正比，Hessian矩阵H在关键点的比例尺和位置计算为：

其中导数Dxx，Dxy，Dyy是通过获取比例空间中相邻样本点的差来计算的。

幸运的是，直接计算H的特征值有点慢，这里我们只关注其两个特征值之比，而不关注具体的特征值。假设两个特征值均为正，并且当λ和rλ且r≥1时，它们满足：

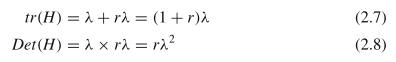
我们可以进一步获得：

由于r≥1，tr(H)2 / Det(H)与r一起单调增加。结果，我们只需要在tr(H)2 / Det(H)上设置一个阈值即可丢弃具有较大r的点，该点对应于较大的主曲率和较小的曲率。在SIFT的实现中，将r设置为10。如果Det(H)为负(它将具有负特征值)，则将关键点视为不是极值而将其丢弃，但这很少发生。

关键点检测的最后一步是为每个关键点分配方向。请注意，此步骤是可选的。如果任务不必旋转处理图像，则可以跳过此步骤，从而在效率和准确性上获得更好的性能。否则，此步骤对于实现旋转不变性很有用。关键点的方向取决于其范围从圆形邻域计算得出。具体来说，给定一个关键点(x，y，σ)，我们首先从尺度空间中取出最接近σ的高斯模糊图像。在此图像中执行以下所有操作，以便缩放不变。然后，从关键点周围的局部圆形区域计算出梯度方向的直方图(将360度量化为36个bin)。该圆形区域的半径设置为4.5σ。除此区域中每个样本点的梯度幅度外，还将其与直方图相加时，还使用高斯函数(标准差为1.5σ)对其进行加权。最后，将对应于该直方图中最高峰的方向作为该关键点的方向。对于在最高峰的80％之内的其他峰，其相应方向也将作为关键点的方向。因此，对于一个关键点，它可能会分为几个关键点，它们的方向不同。值得指出的是，在计算与峰相对应的方向时，将抛物线拟合到以峰为中心的3个直方图块中，以对峰位置进行插值以获得更好的精度。

2.1.3功能描述

在关键点检测中，将检测每个关键点及其位置，比例和方向。这些参数可用于构造局部描述符，以比例和旋转不变的方式描述此关键点。简而言之，如图2.2所示，通过将这些参数定义的局部区域划分为4×4网格，然后计算这些网格中的梯度方向直方图，最后将这些直方图连接在一起，进一步构造为单位向量作为描述符。

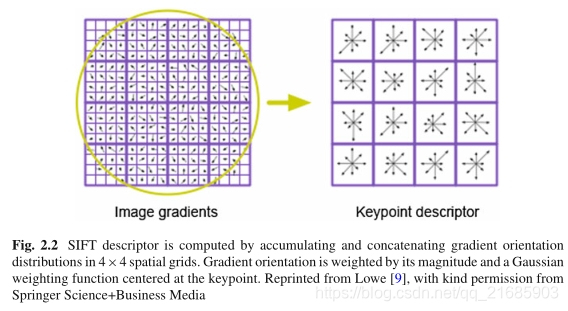
图2.2通过累积和级联4×4空间网格中的梯度方向分布来计算SIFT描述符。 梯度方向由其大小和以关键点为中心的高斯加权函数加权。 经Springer Science + Business Media的许可，从Lowe [9]转载

首先，类似于关键点方向的计算，我们必须根据关键点的尺度在尺度空间中取出高斯模糊图像。在此图像中构造了SIFT描述符，以确保比例不变。然后，根据关键点比例σ从图像中取出关键点位置周围具有16×16个采样点的局部区域。对于每个采样点，计算其梯度大小和方向。请注意，要实现旋转不变性，这些采样点的坐标和梯度方向将相对于关键点方向进行旋转。使用标准方差为1.5W(W是局部区域的宽度)的高斯加权函数对每个采样点的幅度进行加权，以更加强调关键点附近的那些采样点。同时，为了鲁棒地在这些采样点中移动以及对一些空间信息进行编码以提高区别性，将16×16局部区域进一步划分为4×4网格。在每个网格中，基于梯度大小和高斯权重计算梯度方向的直方图。将所有直方图连接在一起以形成128维描述符。为了处理突然的照明变化，使用了两步归一化。首先将128描述符标准化为单位长度。然后，任何大于0.2的元素将被裁剪为0.2。裁剪后的向量将重新标准化为单位长度，作为最终的SIFT描述符。

从上面的过程中，我们可以看到SIFT实际上是累积了一个空间位置和梯度方向的3D直方图，并由aGaussian函数和梯度幅度加权。为了提高其鲁棒性并避免边界效应，使用了软分配。通过这种方式，采样点根据其到每个仓中心的距离，对128维SIFT描述符中的8个相邻仓起作用。

值得指出的是，Dalal和Triggs [4]提出的行人检测著名的定向直方图(HoG)具有与SIFT描述子相似的基本思想。它们都在描述的区域中的不同空间区域上积累定向的梯度响应，该梯度响应由梯度幅度加权。不同之处在于，HoG使用更多的重叠单元来收集定向梯度的直方图，这些直方图根据较大区域(块)中的“能量”进行了归一化。 HoG检测窗口/所描述的区域被分成许多块以获得判别表示。如今，HoG已经成为一种特征提取的标准技术，可用于对象检测，而不仅仅是行人检测。

2.2加速的鲁棒功能(SURF)

尽管SIFT对许多几何和光度转换具有区分性和鲁棒性，但计算速度较慢，这在一定程度上限制了其应用。为了减轻这个问题，Bay等人[2]提出了一种通过修改SIFT以使其适应于积分图像的SIFT的快速替代方案，该算法可以非常快速地进行计算。
他们的方法称为加速鲁棒特征(SURF)。它的算法流水线与SIFT相似，主要包括三个步骤：(1)输入图像的比例空间表示； (2)在尺度空间中检测SURF关键点(兴趣点)； (3)为关键点分配方向并构造其SURF描述符。我们将在以下各节中详细介绍每个步骤。

2.2.1积分图像

在正式介绍SURF的这些算法步骤之前，我们先简单介绍一下SURF的核心积分图像技术。根据定义，积分图像IΣ在位置(x，y)的输入是输入图像I中所有像素的总和，该像素由原点(图像的左上角)和(x，y)形成的矩形区域内。因此，给定大小为m×n的图像I，其积分图像IΣ可计算为：

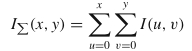
积分图像的优点在于可以快速计算出任何直立的矩形区域上的强度之和。可以看出，一旦计算出积分图像，对于任何直立的矩形区域，无论区域的大小如何，都只需要三个加法即可获得其求和强度。当必须频繁获取整个区域的强度总和并且必须在较大的区域上进行操作时(这是SURF面临的情况)，这非常有用。

2.2.2 SURF中的尺度空间表示

为了检测具有不同比例的兴趣点，人们必须诉诸于输入图像的比例空间表示。通常，像SIFT一样，将比例尺空间实现为图像金字塔[9]，其中，使用高斯核反复对输入图像进行平滑处理，然后进行二次采样以获得更高级别的金字塔。与通常的策略不同，SURF提议通过反复增加滤镜尺寸来反复减小图像尺寸，从而获得输入图像的比例尺空间表示，如图2.3所示。

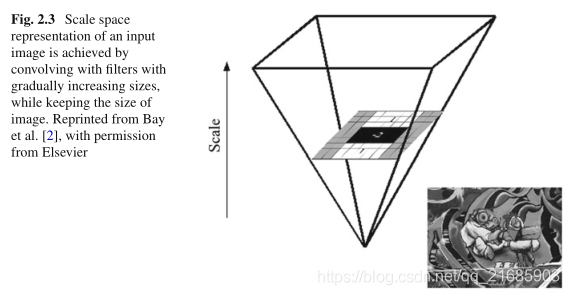
图2.3输入图像的比例空间表示是通过与尺寸逐渐增大的滤镜进行卷积来实现的，同时保持图像的尺寸。 经Elsevier许可，转载自Bay 等人 [2]

除SIFT中使用的高斯差(DoG)所近似的尺度高斯标准化拉普拉斯算子(LoG)外，Hessian矩阵的行列式是另一种用于检测尺度不变兴趣点的流行度量。 SURF的兴趣点检测器基于这种行列式的计算，但是具有一些近似值，因此计算速度非常快。从数学上讲，图像I中点x上的点x的黑森州矩阵可以通过以下公式计算：

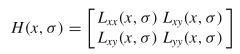
其中Lxx(x，σ)是二阶高斯导数与x中的图像I的卷积，而σ是高斯的标准方差。对于Lxy(x，σ)和Lyy(x，σ)类似。

为了使用积分图像有效地计算Hessian响应，SURF使用由几个盒式滤波器组成的滤波器来近似二阶高斯导数，如图2.4所示。由于这些盒式滤波器对图像的卷积仅需基于积分图像进行几次加法即可计算，因此计算近似的Hessian矩阵非常快速。形式上，近似的Hessian矩阵ˆH(x，σ)由下式定义：

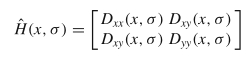
其中Dxx(x，σ)，Dyy(x，σ)和Dxy(x，σ)分别是近似滤波器与图像I的卷积。

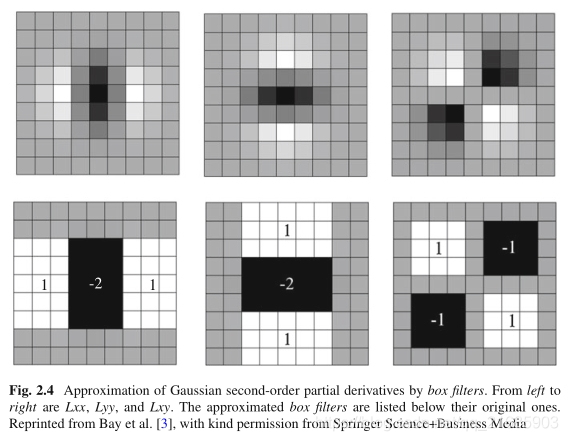
图2.4高斯二阶偏导数通过箱形滤波器的逼近。 从左到右是Lxx，Lyy和Lxy。 近似的框式过滤器在其原始过滤器下面列出。 转载自Bay等。 [3]，经Springer Science + Business Media的友好许可

Hessian矩阵的行列式可以用作斑点点的响应，即R(x，σ)= LxxLyy-Lxy2≈DxxDyy-(0.9Dxy2)。为了保证任何滤波器大小的Frobenius范数不变，用相应的滤波器大小对R(x)进行归一化。这对于标度空间分析很重要，因为它可以防止较大比例的滤波器响应降低。基于此测量，将通过非最大抑制跨尺度检测兴趣点，这将在下一部分中进行描述。可以看出，只有Dxx(x，σ)，Dyy(x，σ)和Dxy(x，σ)与兴趣点检测相关，因此实际上生成了三个比例空间。一个用于Dxx(x，σ)，另外两个用于Dyy(x，σ)和Dxy(x，σ)。

与SIFT中使用的八度音阶结构类似，SURF也使此结构适应于表示音阶空间。具体而言，每个八度音阶包括2的缩放因子，并且包含几个级别，每个级别对应于卷积图像，该卷积图像的卷积与该级别的比例有关。相邻音阶的滤波器大小在一个八度音阶中的常数因子中不同，并且对于相邻八度音阶，此大小差增加了一倍。如前所述，SURF使用盒式滤波器近似二阶高斯导数。 9×9是此近似值的最小框式过滤器大小(对应于σ= 1.2的高斯)，因此它充当标度空间中的最小标度。如图2.4所示，Dxx和Dyy中包含三个部分。为了确保总的过滤器尺寸不均匀，两个连续刻度的每个部分可以增加的最小尺寸为2。结果，整个滤波器为6。因此，在第一个八度音程中，滤波器的大小为9、15、21，…。在接下来的在比例空间中找到极端点的步骤中，可以看出，它需要两个额外的相邻级别来检测某个级别中的兴趣点。因此，每个八度中的第一级和最后一级仅用于辅助目的。同时，由于在标度空间中进行插值以细化兴趣点的标度，因此第一个八度音阶中的最小标度为(9 + 15)/ 2×1.2 / 9 = 1.6。由于一个八度音阶包含比例因子2，因此，第一个八度音阶的最大音阶为3.2，对应于滤波器大小为24，因此，用于兴趣点检测的最后一个有用电平为21(因为(21 + 27)/ 2 = 24)。同样，第二个八度中的滤波器大小为15、27、39、51；第三个八度中的第一个是27、51、75、99，直到输入图像大小不再大于过滤器大小为止。可以看出，此比例尺空间表示中的八度音阶重叠以无缝覆盖所有可能的比例尺。

从标尺空间的上述结构可以明显看出，标尺的采样是相当粗糙的。例如，在第一个八度的前两个级别中，音阶变化为15/9 = 1.67。因此，SURF还提供了一种策略，以花费更多的计算时间来获得具有更精细采样比例的比例空间表示。该策略首先使用线性插值将输入图像加倍。然后，在第一个八度中，其第一级为15×15，而不是原始版本中的9×9。在第一个八度音阶的其余电平中，滤波器的大小为21、27、33、39。其余内容与原始版本中的内容相似。第二个八度从27开始，并增加12倍，对于第三个八度，第四个八度等，依此类推。在比例空间的这种实现方式中，可以发现比例变化为21/15 = 1.4 ，小于1.67。同时，可以通过二次插值获得的最佳比例为(15 + 21)/ 2×1.2 / 9×1/2 = 1.2。

2.2.3尺度不变兴趣点检测

通过在空间和比例空间的3×3×3邻域中应用R(x，σ)的非最大抑制来对兴趣点进行定位。 SURF中使用了[10]中描述的快速非最大抑制技术。基本思想是两个局部最大值在每个维度上至少相隔r个像素，其中r是用于非最大值抑制的邻域半径。因此，不需要检查所有像素。

由于空间网格和比例尺的原始采样所定义的位置不稳定，因此有必要使用其他程序来完善位置。这是通过在与SIFT相同的空间和比例上拟合抛物面来实现插值的。有关详细信息，请参阅第2.1节。在此过程之后，获得具有子像素/子比例精度的最大值，并将其作为检测到的兴趣点。

2.2.4方向分配和描述符构造

为了使SURF描述符对于图像旋转不变，首先基于来自围绕兴趣点的圆形区域的信息来计算可重现的方向。然后，构造与计算的取向对准的正方形区域。最后，从该正方形区域提取SURF描述符。

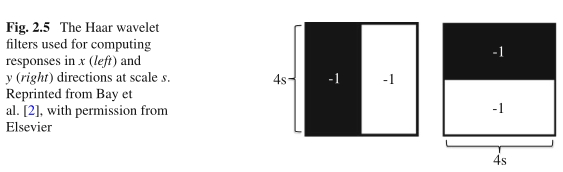
图2.5 Haar小波滤波器用于计算标度s在x(左)和y(右)方向上的响应。转载自Bay等人[2]，经Elsevier许可

为了计算每个兴趣点的可重现方向，使用围绕兴趣点的半径为6s的圆形邻域，其中s是兴趣点的比例。对于该区域中的每个采样点(为了使用积分图像四舍五入为整数)，将计算x和y方向的Haarwavelet响应，分别用dx和dy表示。为了保持标度不变，将采样步骤设置为s。同时，Haar小波的大小也与比例有关，并设置为4s，如图2.5所示。通过使用积分图像，只需要六次操作即可在任何比例下计算x / y方向上的响应。为了更加强调中心采样点，对这些Haar小波响应应用了高斯(σ= 2s)加权函数。然后，将所有这些高斯加权响应映射到以x方向响应为横坐标和y方向响应为纵坐标的2D空间。大小为π/ 3的滑动定向窗口用于对所有点求和，以获得局部定向矢量(请参见图2.6)。最后，将所有滑动窗口中最长的方向向量作为兴趣点的方向。

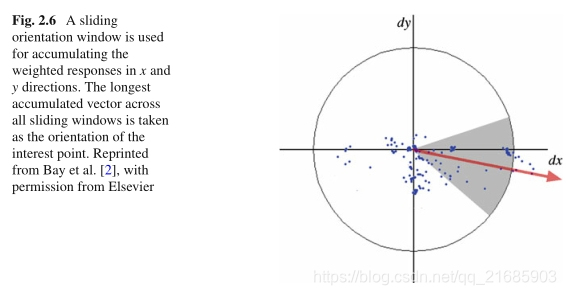
图2.6滑动方向窗口用于累积x和y方向上的加权响应。 所有滑动窗口上最长的累积矢量被当作兴趣点的方向。 转载自Bay等人 [2]，经Elsevier许可

为了提取兴趣点的SURF描述符，它必须构造一个以兴趣点为中心并对齐其方向的正方形区域。该正方形区域的大小设置为20s，采样步长为s，以获得尺度不变性。然后将正方形区域规则地划分为4×4子区域，以保留重要的空间信息以实现独特性。对于该平方区域中的每个采样点，计算其在水平和垂直方向(dx和dy)的Haar小波响应。请注意，“水平”和“垂直”是根据兴趣点的方向定义的。与方向分配中使用的Haar小波不同，此处的滤波器大小设置为2s。为了提高效率，它们首先在未旋转的图像中计算出来，然后根据兴趣点的方向旋转，而不是旋转图像并计算这些Haar小波响应。然后将它们映射到4维向量，以编码有关强度变化极性的信息，即(dx，| dx |，dy，| dy |)。最后，将这些4维向量在每个子区域上求和，并以以兴趣点为中心的高斯函数(σ= 3.3s)加权。将所有16个子区域中所有累积的向量连接在一起，以形成SURF描述符(64维)，将其标准化为单位长度，以实现对比度变化的不变性。使用高斯函数加权样本点的响应是为了增加对定位误差和几何变形的鲁棒性。

为了进一步提高描述符的判别能力，SURF描述符的另一种版本是将Haar小波响应映射到8维向量：((dx，| dx |)dy> 0，(dx，| dx |)dy≤0 ，(dy，| dy |)dx> 0，(dy，| dy |)dx≤0)∈R8，其中(dy，| dy |)dx> 0表示仅当dx> 0时才有效，否则设置为(0，0)。其他条款也是如此。此替代版本的尺寸为128。它更具特色，计算速度稍慢，但匹配速度较慢，由于其尺寸较大，因此需要存储两次。

2.3本地二进制模式及其变体

另一个非常流行且广为人知的本地功能是本地二进制模式(LBP)系列。自从1990年代首次引入基本的LBP以来，LBP方法在过去的二十年中发展了很多，从扩展，相关理论到各种新应用。

最初，LBP [11]被提出来描述纹理，其特征可能在于强度或颜色的不均匀分布，并应用于纹理分类和分割。由于其良好的性能和计算的简便性，LBP在计算机视觉社区中迅速得到普及，并已成为在现实世界中应用(不仅限于与纹理相关的应用)中进行图像处理的广泛使用的运算符。

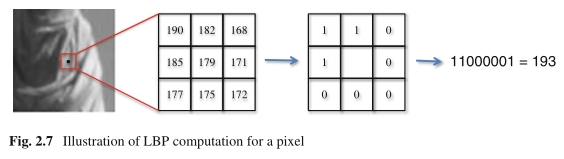
图2.7像素的LBP计算示意图

通过将LBP算子应用于图像，每个像素由整数标签表示(例如，原始LBP中具有3×3邻域配置的256个不同标签)，该标签对于单调照明变化具有鲁棒性。这些标签中的每一个都称为LBP模式。在原始版本的LBP [11]中，像素的LBP模式是通过将3×3区域中每个相邻像素与中心像素的强度进行比较来计算的，如图2.7所示。这样的比较将导致一个具有8个元素的位串，因此，总共28 = 256个不同的可能标签。在数学上，以下[12]给出了LBP的更通用定义：

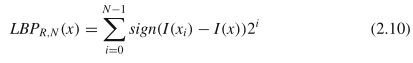
其中sign(x)是符号函数，当输入大于0时输出1，否则输出0。R定义半径为R的像素x的圆形邻域，N表示该圆上用于采样的规则采样点数LBP计算。在任何情况下，采样点都不会位于离散像素中，则使用双线性插值来获取其强度。

根据实验结果，Ojala等[12]提出了LBP的统一模式。基于LBP模式的定义，他们进一步定义了模式的均匀性度量，即其二进制表示形式中从0到1或从1到0的按位转移的数量。注意，在此定义中，将模式视为循环模式。均匀性度量可以表述为：

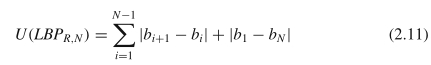
其中bi是LBP位串的第i位。

根据这种均匀性度量，Ojala等人将均匀性度量不大于2的LBP模式定义为均匀性模式：LBPR,Nu = {LBPR,N | U(LBPR,N)≤2}。对于N位的LBP模式，有N(N − 1)+ 2个均匀模式。通常，对于其余的非均匀模式，将它们一起视为单个标签(模式)。因此，通过均匀的图案，LBP的直方图可以从2N个信箱减少到N(N -1)+ 3个信箱，从而大大减少了用于特征描述的维度。同时，发现均匀图案在自然图像中更稳定并占主导地位。例如，根据Ojala等人对纹理图像进行的实验，当使用(R = 1，N = 8)LBP邻域时，所有图案中将近90％是均匀图案。在面部图像中也观察到类似的统计结果[1]。

为了实现旋转不变的表示，将LBP模式循环移位到其最小整数值[14]，如下所示：

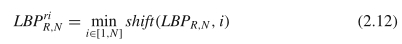
其中shift(LBPR,N，i)指示以i位向LBPR,N右移的操作(以循环方式)。对应于该最小整数值的模式LBPR,Nri 被定义为旋转不变LBP。在N = 8的情况下，存在36个旋转不变LBP。我们可以看到，旋转不变的LBP实际上将一组LBP模式映射为一个，因此可以降低判别力。根据LBPR,N和LBPR,Nri的定义，理论上，这样的旋转不变性仅在角度2π×i / N，i = 1…，N −1时可用。但是，实际上，它在任何角度都非常坚固。

在统一模式集合中，除了全为1s和全为0s的模式之外，它还包含N-1组模式。每组包含i(1≤i <N)1s的N个模式，所有模式仅在旋转时有所不同。因此，如果不考虑旋转，则每个组实际上对应一个模式。结果，总共有N + 1个不同的这种模式，称为旋转不变的均匀模式。它们可以通过以下方式制定：

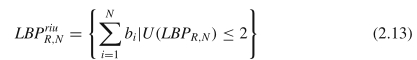
类似于均匀图案的情况，不属于任何旋转不变均匀图案的所有其他图案都被视为单个图案。

已经提出了LBP的许多扩展，以提高其鲁棒性和判别能力，或使其适应新的计算机视觉任务。这些变体包括对LBP的许多部分的改进，例如，将其他互补特征合并到LBP中，更改了其阈值和强度比较的方法，扩展了多尺度分析，使其能够处理颜色信息，将其扩展到时空区域等。在本节中，我们将简要介绍一些我们认为对LBP开发很重要的变体。对于LBP变体的全面回顾和介绍，我们请有兴趣的读者参考[13]。

局部Gabor二进制模式：局部Gabor二进制模式(LGBP)[17]是一个非常好的局部特征，广泛用于面部识别。通过使用Gabor滤波和LBP运算符，它可以有效地组合本地和区域信息。具体地，首先通过一组具有不同比例和方向的Gabor滤波器对面部图像进行滤波，以便在比例和方向的板范围内获得丰富的外观信息。然后，将LBP运算符应用于这些Gabor滤波图像中的每一个(仅使用幅度)，并针对每个Gabor滤波图像从输入面部图像划分的空间子区域获得一组直方图。最后，所有直方图都作为LGBP特征连接在一起。
其管线如图2.8所示。但是，此方法的缺点是此类表示的维数很高，例如具有5个比例尺和8个方向，这导致人脸表示的尺寸是使用原始LBP时的40倍。

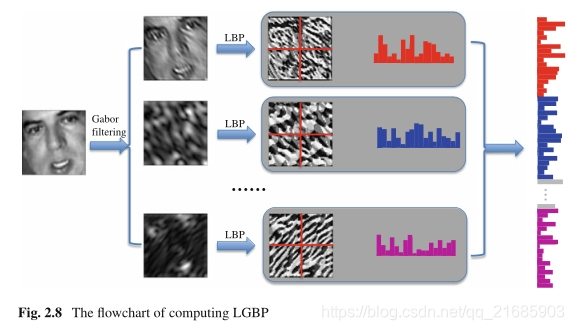
图2.8 LGBP计算流程图

多尺度块局部二进制模式：人脸识别中另一个广泛使用的LBP变体是多尺度块局部二进制模式(MB-LBP)[8]。它扩展了原始的LBP以对较大区域中的信息进行编码，从而覆盖了面部图像中的微观和宏观结构。因此，期望更高的判别力。
MB-LBP的基本思想是使用s×s子区域的平均强度来代替原始LBP中中心像素/相邻像素的强度。 s的大小对应于MB-LBP的大小。通常，几种尺度的MB-LBP一起使用，然后是Adaboost算法[5]以选择最具区分性的特征进行人脸识别。图2.9给出了使用3×3子区域的示例。

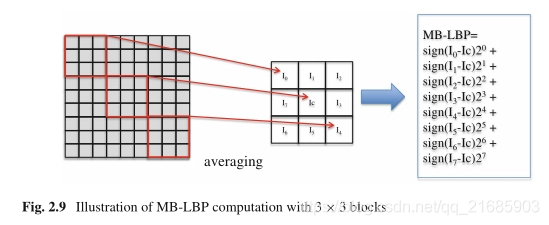
图2.9 3×3块的MB-LBP计算示意图

MB-LBP提出的LBP的另一种修改是使用从训练数据中获得的统计有效的统一模式集。更具体地说，首先针对每个比例获得MB-LBP模式的直方图。然后，对于每个比例，将获得与前N个箱相对应的MB-LBP模式作为N个均匀的MB-LBP模式，并接收从0到N-1的标签。所有其余模式共享一个标签N。如果将其分别处理，则获得的一组统一的MB-LBP模式将具有较大的冗余度。用于面部识别的最终集合由Adaboost算法选择。

局部三元模式：为了使LBP对强度的微小变化/噪声更鲁棒，该变化/噪声通常发生在平坦或接近均匀的图像区域和阴影区域，Tan和Triggs [15]将LBP中的二元模式修改为三元模式，因此称为本地三态模式(LTP)。在LBP中，它将阈值的强度设置为中心像素的强度，从而为附近的每个采样点计算一个二值位代码(0或1)。在LTP中，它通过对两个强度进行阈值计算，为每个采样点计算三值代码(−1、0、1)，如下所示：

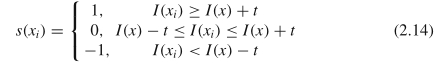
其中，I(x)是中心像素的强度，xi是x附近的第i个采样点，t是预定义的偏移量，以生成两个阈值，通常将其设置为5。将N个采样点的所有值连接在一起一起用作中心像素的LTP代码。

直观地，N个采样点可以形成总共3N个可能的LTP代码。如此大的范围将进一步使直方图表示非常稀疏，这可能会降低其判别能力并使其对噪声敏感。由于这些原因，N个三个值代码s(xi)，i = 1，…，N根据其符号分为两组，得到两个局部二进制模式，如图2.10所示。这两个部分分别用于获得所描述区域的表示，例如直方图。这些表示最终被串联为单个特征向量。

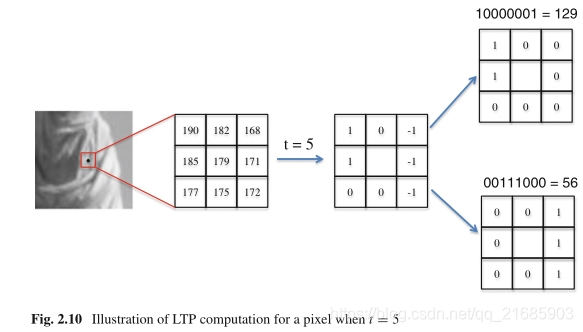
图2.10 当t = 5时像素的LTP计算图

LTP的一个缺点是，使用恒定偏移量t生成两个阈值会使所计算的LTP代码在强度的标度变化下不会不变。廖等人[7]注意到此问题，并提出了比例不变LTP(SILTP)来解决此问题。 SILTP的基本思想非常简单，即用与中心像素强度成比例的值替换LTP中的偏移量t。同时，为了避免将三进制代码分成两个二进制代码，他们使用两位来表示获得的三个值。然后将所有采样点的二进制代码连接起来，就可以形成一个像素的SILTP表示形式。在数学上，SILTP运算符可以表示为：

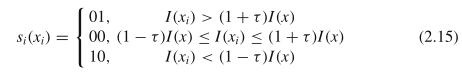
其中τ是预定义的比例因子，表示可以容忍多少中央像素的强度。显然，SILTP运算符对强度是尺度不变的。

中心对称的本地二进制模式：尽管LBP具有高判别力和对光照变化的鲁棒性，但其高维度使其不适合描述关键点周围的感兴趣区域，为此通常需要低维度描述符，例如128维SIFT描述符。甚至均匀LBP的直方图仍然太长，无法在兴趣区域描述符中使用。有人可能会争辩说，如果使用原始LBP，我们可以将整个兴趣区域中LBP的直方图作为描述符，其维度为256。但是，这种方法没有在描述符中编码任何空间信息，这对于区分不同的兴趣区域非常重要。因此，其判别能力显着降低，使其无法用于跨不同图像匹配兴趣区域。

尽管存在困难，但LBP抵抗光照变化的良好性能使其对研究感兴趣区域描述的研究人员具有吸引力。受此影响，Heikkila等人[6]修改的LBP在使用8个邻域时总共只有16种可能的模式。在这种情况下，可以将其用于类似于SIFT的特征描述算法中，从而获得高性能的描述符。该修改的核心思想是比较中心对称采样点的强度，而不是比较采样点和中心像素的强度。因此，对于N个邻域采样，仅生成N / 2位，可以将其进一步编码为2N/2维直方图。
修改后的模式称为中心对称本地二进制模式(CS-LBP)。而且，由于在关注区域中可能存在大部分平坦区域，因此有必要使LBP对较小的强度变化具有鲁棒性，因为这经常在带有噪声的平坦区域中发生。为此，CS-LBP操作员在强度比较中引入了可容忍的阈值。综上所述，像素x的CS-LBP运算符可以表示为：

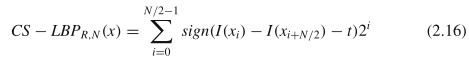
R，N和sign(x)的含义与公式(2.10)中的含义相同。 t是一个平衡噪声容限和CS-LBP判别能力的阈值。 t值越大，其可抵抗强度的湍流越大。但是，要使CS-LBP有区别，就需要较小的t值。在大多数情况下，t的典型设置为3。 I(xi)和I(xi+N/2)是两个中心对称采样点的强度。图2.11描绘了N = 8时LBP和CS-LBP的差异。

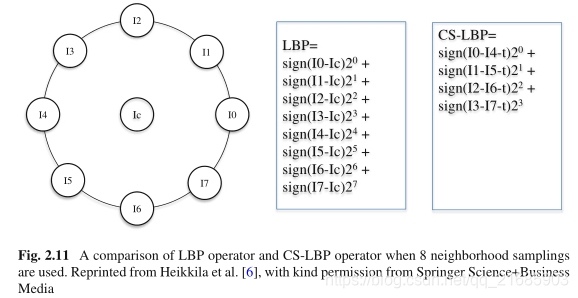
图2.11使用8个邻域采样时LBP算子和CS-LBP算子的比较。 转载自Heikkila等人[6]，得到Springer Science + Business Media的许可

CS-LBP的低维特性使其可以像SIFT一样，通过在划分的子区域中串联直方图来适合兴趣区域描述。实际上，这就是Heikkila等人的方法[6]。确实构造了一个描述符，以结合SIFT和LBP的优势。生成的描述符也称为CS-LBP。除了以下两个区别之外，用于构造CS-LBP描述符的管道与SIFT相似。

(1)它不具有特征加权步骤，该特征加权步骤根据兴趣区域中的每个像素的梯度幅度和SIFT中的高斯函数为其分配权重。他们在[6]中报告的实验结果支持了这一步骤的省略。

(2)在累积CS-LBP值和位置的3D直方图时，通过使用双线性插值将像素分配给其空间中的4个相邻bin。在SIFT中，通过在空间和梯度方向上进行插值，可将一个像素添加到其8个相邻像素中。由于CS-LBP本质上是量化的，因此在构造CS-LBP描述符时不必在此维度上进行插值。

**局部强度顺序模式：**为充分探索像素的相邻采样点之间的强度关系，Wang等人[16]提出了局部强度顺序模式(LIOP)来描述兴趣区域。尽管两者都针对感兴趣区域描述而提出，但是LIOP优于CS-LBP的优点是它不仅可以比较中心对称采样点之间的强度，而且可以比较附近采样点之间的强度。由于采用这种强度比较策略，LIOP比CS-LBP更具区分性，而且LIOP仅使用4个相邻点而不是8个相邻点，同时获得了更好的性能。

给定像素x的4个相邻点x0，x1，x2，x3，它们的强度由I(x0)，I(x1)，I(x2)，I(x3)表示。由于4个强度有24种可能的排列，因此每个排列都可以定义为局部强度顺序模式。局部强度阶次模式可以进一步用24维向量表示，一个元素为1，其他元素为0。因此，通过对x的4个相邻点的强度进行排序，我们可以首先获得一个置换，然后对其进行排列相应的24维向量作为x的局部强度有序模式。请参见第3.3节，以获取更多有关如何使用它来构建健壮且独特的兴趣区域匹配描述符的详细信息。

参考文献

1. Ahonen, T.,Hadid,A., Pietikainen, M.: Face descriptionwith local binary patterns: Application to face recognition. IEEE Trans. Pattern Anal. Mach. Intell. 28(12), 2037–2041 (2006) 2. Bay, H., Ess, A., Tuytelaars, T., Gool, L.V.: SURF: speeded up robust features. Comput. Vis.Image Underst. 110(3), 346–359 (2008)
2. Bay, H., Tuytelaars, T.,Gool, L.V.: SURF: Speeded up robust features. In: European Conference on Computer Vision, pp. 404–417 (2006)
3. Dalal, N., Triggs, B.: Histograms of oriented gradients for human detection. In: IEEE Conference on Computer Vision and Pattern Recognition, pp. 886–893 (2005)
4. Friedman, J., Hastie, T., Tibshirani, R.: Additive logistic regression: a statistical view of boosting.Ann. Stat. 28(2), 337–407 (2000)
5. Heikkila, M., Pietikainen, M., Schmid, C.: Description of interest regions with centersymmetric local binary patterns. In: 5th Indian Conference on Computer Vision, Graphics and Image Processing, pp. 58–69 (2006)
6. Liao, S., Zhao, G., Kellokumpu, V., Pietikainen, M., Li, S.: Modeling pixel process with scale invariant local patterns for background subtraction in complex scenes. In: IEEE Conference on Computer Vision and Pattern Recognition, pp. 1301–1306 (2010)
7. Liao, S., Zhu, X., Lei, Z., Zhang, L., Li, S.: Learning multi-scale block local binary patterns for face recognition. In: International Conference on Biometrics, pp. 828–837 (2007)
8. Lowe, D.: Distinctive image features from scale-invariant keypoints. Int. J. Comput. Vis. 60(2), 91–110 (2004)
9. Neubeck, A., Van Gool, L.: Efficient non-maximum suppression. Int. Conf. Pattern Recogn. 3, 850–855 (2006)
10. Ojala, T., Pietikainen, M., Harwood, D.: A comparative study of texture measures with classification based on feature distributions. Pattern Recogn. 29, 51–59 (1996)
11. Ojala,T., Pietikainen, M.,Maenpaa,T.: Multiresolution gray-scale and rotation invariant texture classificationwith local binary patterns. IEEE Trans. PatternAnal. Mach. Intell. 24(7), 971–987 (2002)
12. Pietikainen, M., Hadid, A., Zhao, G., Ahonen, T.: Computer Vision Using Local Binary Patterns.Springer (2011)
13. Pietikainen, M., Ojala, T., Xu, Z.: Rotation-invariant texture classification using feature distributions.Pattern Recogn. 33, 43–52 (2000)
14. Tan, X., Triggs, B.: Enhanced local texture feature sets for face recognition under difficult lighting conditions. IEEE Trans. Image Process. 19(6), 1635–1650 (2010)
15. Wang, Z., Fan, B.,Wu, F.: Local intensity order pattern for feature description. In: International Conference on Computer Vision, pp. 603–610 (2011)
16. Zhang, W., Shan, S., Gao, W., Chen, X., Zhang, H.: Local gabor binary pattern histogram sequence (LGBPHS): A novel non-statistical model for face representation and recognition.In: International Conference on Computer Vision, pp. 786–791 (2005)

有问题请及时联系博主：Alliswell_WP——https://blog.csdn.net/qq_21685903?spm=1001.2014.3001.5343

第一篇链接：https://developer.jdcloud.com/article/1438?mid=13