一、引言
在配送需求不断增长的背景下,个人配送服务的大规模众包化将对配送市场产生重大影响,且众包定价涉及要素较多;这些变化意味着我们的营业部需要进行更精细化的定价管理,以适应众包人员市场。与自营人员不同,众包骑手的服务质量受到当地当时的人员可用性和成本波动的影响。为了提高骑手服务的揽派效率,降低整体运营经营成本,如何动态定价成为一个可考虑的选择。通过动态定价,可以一定程度的帮助配送站点通过响应配送需求的变化来最大化收入并减少人员短缺;
在日常配送中,动态定价的优势显而易见。然而,在高峰时段或偏远地区,临时性的众包骑手服务比全职骑手更复杂,需要更精细的规划。价格的不确定性可能增加规划和配送的难度。然而,如果众包骑手可以提前储备,那么报价也可以提前规划并完成锁定。这样,配送站点可以规划整个运营周期,并明确骑手服务的成本。这也是从过往一些营销补贴案例中,对于券种选择,触达人员分析的一些思考,只是众包的定价更强调周期性以及地区性,因此仅作为探索;
二、 MDP模型用于动态定价
站点众包骑手的定价主要是基于路区难度系数,历史单均等因素对未来的预测单量进行顺序定价决策。因此,马尔可夫决策过程(MDP)是可以作为一个基础模型。MDP是其他动态定价工作的常用模型,尤其是当与强化学习结合时,如一些经典的充电桩分配问题。在这些案例中,状态空间尽可能多地构建状态变量,并从数据中学习定价策略。然而,由于训练模型需要大量的计算资源来训练历史每天的运单数据与计费数据,强化学习的优先级会较低。在此选择一些规则叠加聚类模型能更好的帮助我们进行历史数据特征选择和模型训练。最后,可以参考其余案例使用泊松过程来模拟每个周期内单量需求的情况。通过将泊松过程应用于我们的离散时间模型在线动态定价中,并且可以定义为一种离散化误差;
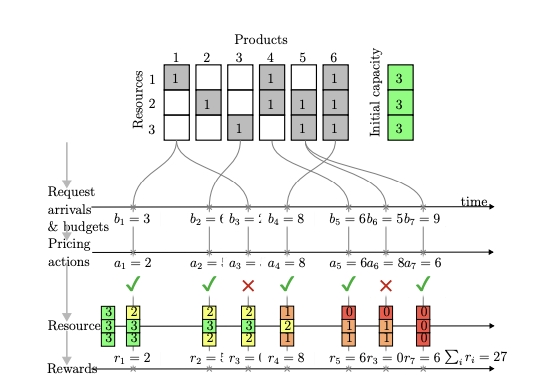
如图所示,可以拆解为这几步:
资源矩阵:在众包骑手定价中,资源矩阵可以表示为不同时间段内可用的骑手资源。
产品定义:产品可以定义为特定时间段内的骑手服务组合。例如,产品 [1, 1, 0] 可以表示在三个时间段中的第一个和第二个时间段内提供骑手服务。
请求到达和预算:站点在不同时间提出对骑手服务的请求/需求,并提供他们愿意支付的报价预算(b1 到 b7)。
定价行动:营业部根据当前的骑手可用性和市场需求,采取动态定价策略(a1 到 a7)。每个定价决定都是基于当前资源状态和预期需求。
接受与奖励:当客户接受报价(即,当他们的预算 bi 大于或等于定价 ai 时,用绿色的 ✓ 表示),营业部获得一个奖励 ri。这可以是收入或其他绩效指标。同时,骑手资源的可用性根据所售产品的需求而减少。
资源管理:营业部需要持续监控和调整骑手的分配,以确保在满足需求的同时最大化收入。这包括在高需求时段提高价格,或在低需求时段进行调价处理。
1. 众包动态定价问题描述
众包骑手服务的动态定价涉及为不同的配送产品(计费类型)在线设置最优或接近最优的价格,因为站点下不同路区、不同地址导致的报价都不尽相同。我们的配送站点将其资源——一组配送站的配送能力——组合成提供给客户的产品,例如小时达等。 同样的,对于不同的配送产品,公司内部的计费形式和计费价格都不尽相同,需要我们更精准更合理的进行资源分配;
由于对不同的配送产品的需求事先是未知的,但我们拥有关于揽派送的历史数据、未来单量的一个粗粒度的预测数据以及不同时间段下单均成本变化数据。我们的目标是以一种方式可以定价每个到达该站点的揽派产品请求,以最大化目标函数,同时考虑需求的不确定性(季节性,大促活动等)。
那么在定价策略中,骑手和站点分别对应供应方和需求方的不同角色:
骑手(供应方):骑手是提供服务的主体,因此他们代表供应方。他们的可用性、工作时间、以及他们愿意接受的报酬水平都是供应方的关键因素。骑手的数量和他们的工作时间限制了站点能够提供的服务数量。
站点(需求方):站点需要管理和激励骑手,以满足客户的需求,因此在某种程度上站点也可以被视为需求方。站点需要制定价格策略来吸引足够的骑手,同时也要考虑客户的需求和支付意愿。站点通过定价策略来平衡骑手的供应和客户的需求。
问题的供应方由一组 ( n ) 个资源组成,这些资源可以组合成 ( m ) 个可供出售的配送产品。每个产品由一个向量 表示,其中的元素规定了产品中使用的各个资源的数量。这些产品的可用性受到资源初始容量 ( ) 和不同资源销售期长度 ( ) 的限制,这些长度决定了每个资源及其所在产品在何时之后不再可售(表示骑手在特定时间段内可用的时间窗口。在此时间之后,骑手可能不再可用,类似于资源过期。)。
问题的需求方通过一个非齐次复合泊松计数过程 () 来建模,该过程模拟了不同时刻对于不同产品请求的到达,以及不同产品的有限内部客户估值的分布 ( )。即站点需要在骑手的可用性和成本之间找到平衡。
2. MDP模型
在描述了众包动态定价问题后,我们将尝试开发一个马尔可夫决策过程(MDP)模型,以确定定价策略 ( )。定价策略是一个映射,它将价格 (a) 分配给站点-时间对 (),并结合骑手资源的当前可用和计划中的未来容量 (c)。
在我们的MDP中,定义为一个五元组 ((S, T, R, A, s_0)),骑手从某个初始状态 开始。每个状态捕捉当前的时间步、正在请求的站点以及当前可用的骑手数量。骑手为请求的站点提供一个价格 () ,采取一个行动,导致转移到一个新状态 ( )。然而,转移并不是确定性的,因为尚不清楚骑手是否会接受或拒绝价格以及下一个站点请求是什么。通过将随机需求过程 () 和骑手内估值的分布 () 拟合到历史数据,我们可以估计转移概率 (,该概率决定了在状态 (s) 下采取行动 (a) 时达到状态 (s') 的可能性。状态之间的转移还会为骑手带来由函数 (R(s, a, s')) 决定的奖励。
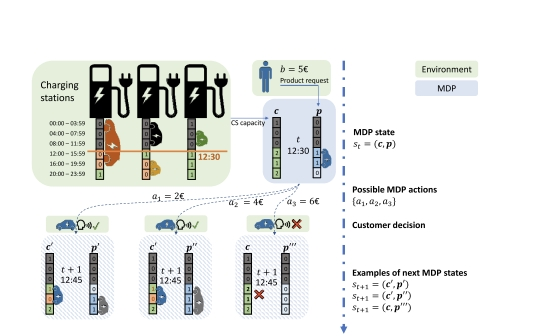
从资料中查询到的关于电动汽车充电动态定价的马尔可夫决策过程(MDP)状态的示意图。该图展示了资源在其销售期结束后的过期情况(容量和产品向量中的灰色部分)。蓝色方块表示MDP状态。在时间步 (t),充电站的容量通过容量向量 (c_t) 表示。向量的元素代表相应时间段(绿色方块中的时间范围)内的可用充电容量。从上一个时间步开始到达的可能充电会话预约请求由向量 (p_t) 表示,其中1表示请求的时间段。基于三个状态变量 (c_t)、(t)、(p_t),定价策略提供一个动作 (a),即充电价格,用户可以接受(底部的前两个状态)或拒绝(右侧的状态)。然后状态转移到下一个时间步(转移函数的详细信息在图4中说明)。接受的充电请求会导致容量值减少。下一个充电会话预约被输入到新状态中。注意,时间步的分辨率必须比充电时间段更精细。灰色显示了关于充电容量和会话向量 (c_t) 和 (p_t) 的过去信息。
而如果我们的项目需要进行相关的框架复用,可以类比骑手资源在其服务期结束后的过期情况(在容量和任务向量中的灰色部分)。蓝色方块表示MDP状态。
在时间步 (t),骑手的可用数量通过容量向量 (c_t) 表示。向量的元素代表相应时间段内可用的骑手数量。从上一个时间步开始到达的可能订单请求由向量 (p_t) 表示,其中1表示请求的时间段。
基于三个状态变量 (c_t)、(t)、(p_t),定价策略提供一个动作 (a),即服务价格,用户可以选择接受(底部的前两个状态)或拒绝(右侧的状态)。然后状态转移到下一个时间步(转移函数的详细信息可以通过类似的图进行说明)。接受的订单请求会导致可用骑手数量减少。下一个订单请求被输入到新状态中。
在调整后的框架下:
容量向量 (c_t):表示在不同时间段内的可用骑手数量。
订单请求向量 (p_t):表示在不同时间段内的订单请求情况。
定价策略 (a):根据当前状态决定的服务价格。
状态转移:订单被接受后,骑手的可用数量会减少,未被接受的订单则不影响骑手数量。
2.1 状态空间
众包项目中,MDP的状态空间 (S) 由状态 (s = (c, t, p)) 组成。这里,(c) 表示当前时刻可用的骑手资源数量,(t) 是离散化的时间步,(p) 是客户在该时间步请求的产品类型。通过将整个服务时间段(0, max(T))离散化为 (k) 个时间步,我们确保状态空间是有限的。虽然可以使用连续时间MDP,但这会增加问题的复杂性,并使解决方案更难以实现。客户请求到达时间是连续的,但在我们的模型中被视为离散事件。我们假设在相似时间到达的客户请求表现出相似的行为,即需求随时间以分段连续的方式变化,具有有限的不连续性。
2.2 动作空间
MDP的动作空间 (A) 是骑手可以提供给客户的可能价格集合。虽然理论上价格集合可以是连续的,但在实践中,我们假设价格是一个有限集合。这种离散化反映了大多数服务提供商在定价时的做法。特别地,有一个特殊的价格 (a = \infty),表示拒绝动作,因为没有客户会接受无限高的价格。当骑手资源不足以满足请求时,采用此动作。
2.3 奖励函数
MDP的奖励函数 () 确定了通过采取动作 (a) 从 (s_t) 转移到 (s_{t+1}) 所获得的奖励。若目标是最大化收入,则奖励为提供给客户的价格。当客户接受报价时,奖励为动作 (a) 的值,否则为0。成功的交易意味着骑手资源从 (c) 减少到 (c - p)。
2.4 转移函数
转移函数 () 是MDP模型中最复杂的部分,它决定了采取动作 (a) 后系统如何从状态 (s_t) 转移到 (s_{t+1})。此函数由客户请求的到达过程 (D(t)) 和客户对产品的内部估值分布 () 决定。在状态 (s_t = (c, p)) 中,骑手为客户请求的产品 (p) 选择一个价格 (a)。客户接受报价的概率由估值分布 () 的补充累积分布函数 决定。
客户请求的到达过程 (D(t)) 基于复合泊松计数过程 (),假设客户到达时间具有无记忆性。我们将泊松过程离散化为多类伯努利过程 (D(t)),在每个时间步最多允许一个产品请求。通过选择适当的时间步数 (k),确保离散化过程 (D(t)) 能够很好地近似泊松过程 ()。
三. MDP模型的离散需求过程
我们尝试使用了一个离散需求过程来模拟每个客户请求的泊松到达过程。
离散需求过程的定义:
假设整个服务时间段 ((0, T)) 被缩放为单位时间段 ((0, 1)),这可以通过简单的时间线重新缩放实现。
对于每种客户请求的产品 (p \in P),我们假设有一个泊松计数过程 (N_p(\tau)),其到达率为 (\lambda_p),用于生成该产品的请求到达时间。
所有产品请求的到达时间可以被视为一个复合泊松过程 (N(\tau)),其强度为 (\lambda = \sum_{p \in P} \lambda_p)。
离散化的必要性:
因为时间被离散化为 (k) 个时间步,我们需要用离散的伯努利过程来逼近泊松过程的到达。
伯努利过程是一系列伯努利试验,定义为 (k) 次试验和每次试验中任何请求到达的概率 (p)。
这种逼近基于泊松过程是通过保持 (kp = \lambda) 不变并让 (k \to +\infty) 的伯努利过程序列的极限。
单个产品请求的分配:
我们可以通过根据概率分配产品索引来重建单个产品的到达过程。 在伯努利过程中,可以通过采样离散分布来将到达分配给产品类型。
逼近质量取决于将连续服务时间段 ((0, 1)) 划分为 (k) 个时间步的值 (k)。
离散需求过程的期望请求数量与泊松过程的期望到达数量在((0, 1))区间内相匹配,因此在这个指标上两者没有差异。
以下是模拟的伪代码,供参考
# 输入参数
stations = [s1, s2, ..., sn] # 站点集合
riders = [r1, r2, ..., rm] # 骑手集合
products = [p1, p2, ..., pk] # 产品集合
zones = [z1, z2, ..., zl] # 路区集合
lambda_p = [λ1, λ2, ..., λk] # 各产品的到达率
historical_prices = {...} # 历史报价数据
historical_volumes = {...} # 历史单量数据
predicted_volumes = {...} # 预测单量数据
pricing_types = ["fixed", "dynamic", "promotional"] # 计费类型
# 时间步设置
T = 1 # 单位时间段
k = 100 # 时间步数
# 初始化请求到达矩阵
requests = [[[[0 for _ in range(k)] for _ in range(len(zones))] for _ in range(len(products))] for _ in range(len(stations))]
# 模拟请求到达过程
for t in range(k):
for station in stations:
for product_index, product in enumerate(products):
# 预测到达率调整
adjusted_lambda = adjust_lambda(lambda_p[product_index], historical_volumes, predicted_volumes, station, product)
# 计算每个时间步的到达概率
p = adjusted_lambda / k
# 在当前时间步内是否有请求到达
if random_bernoulli(p):
# 确定请求的路区
zone_index = sample_zone_distribution(zones, historical_volumes, station, product)
# 增加对应产品和路区的请求计数
requests[stations.index(station)][product_index][zone_index][t] += 1
# 动态定价策略
def dynamic_pricing(station, product, zone, time_step):
# 使用历史报价和单量调整价格
base_price = historical_prices[(station, product, zone)]
demand_factor = calculate_demand_factor(historical_volumes, predicted_volumes, station, product, zone, time_step)
# 定价策略:基于历史数据和当前需求
if pricing_types[product] == "dynamic":
price = base_price * (1 + demand_factor)
elif pricing_types[product] == "promotional":
price = base_price * (1 - 0.1) # 例如促销打九折
else: # fixed
price = base_price
return price
# 辅助函数:伯努利试验
def random_bernoulli(probability):
return random.uniform(0, 1) < probability
# 辅助函数:从路区分布中采样
def sample_zone_distribution(zones, historical_volumes, station, product):
# 根据历史单量在不同路区的分布进行采样
zone_distribution = calculate_zone_distribution(historical_volumes, station, product)
random_value = random.uniform(0, 1)
cumulative_sum = 0
for index, probability in enumerate(zone_distribution):
cumulative_sum += probability
if random_value < cumulative_sum:
return index
return len(zones) - 1 # 返回最后一个索引作为默认
# 辅助函数:调整到达率
def adjust_lambda(base_lambda, historical_volumes, predicted_volumes, station, product):
# 根据历史和预测数据调整到达率
adjustment_factor = predicted_volumes[(station, product)] / historical_volumes[(station, product)]
return base_lambda * adjustment_factor
# 输出请求到达矩阵和价格策略
print(requests)
for station in stations:
for product in products:
for zone in zones:
for t in range(k):
price = dynamic_pricing(station, product, zone, t)
print(f"Price for {station}, {product}, {zone} at time {t}: {price}")
四. 使用蒙特卡罗树搜索(MCTS)
蒙特卡罗树搜索(Monte Carlo Tree Search, MCTS)是一种用于决策过程的启发式搜索算法,广泛应用于博弈论和其他复杂决策问题。MCTS通过随机模拟来探索可能的决策路径,逐步构建决策树,以找到最优策略。以下是MCTS的基本组成部分和工作原理:
选择(Selection):
从根节点开始,使用选择策略(如UCB1,Upper Confidence Bound for Trees)在树中选择一个子节点,直到到达一个未完全扩展的节点。
UCB1策略通过平衡探索(探索不太确定的节点)和利用(利用当前已知最优的节点)来选择节点。
扩展(Expansion):
如果选择的节点不是终止状态且可以扩展,则添加一个或多个子节点。每个子节点表示一个可能的动作或状态。
仿真(Simulation/Rollout):
从扩展的节点开始,进行随机模拟直到达到终止状态。这个过程通常称为“rollout”。
在仿真过程中,随机选择动作来模拟未来的可能路径,以估计该路径的潜在奖励。
回溯(Backpropagation):
将仿真得到的奖励回溯更新到经过的每个节点。更新节点的统计信息,如访问次数和平均奖励。
这种更新有助于逐渐提高对不同路径的估计准确性。
在一些复杂系统中,MDP可以用于建模和提供初步策略,而MCTS可以在实时操作中进行具体的决策优化和调整。这种结合可以充分利用两者的优势,适应不同的需求和约束。
下面是探索过程中的脱敏伪代码:
function MCTS(root_state, iterations):
root_node = CreateNode(state=root_state)
for i from 1 to iterations do:
# Selection
node = root_node
while node is fully expanded and not terminal(node) do:
node = BestChild(node, exploration_param)
# Expansion
if not terminal(node) then:
node = Expand(node)
# Simulation
reward = Simulate(node.state)
# Backpropagation
Backpropagate(node, reward)
return BestAction(root_node)
function CreateNode(state):
return Node(state=state, parent=None, children=[], visits=0, total_reward=0)
function BestChild(node, exploration_param):
best_score = -Infinity
best_child = None
for child in node.children do:
exploit = child.total_reward / child.visits
explore = exploration_param * sqrt(log(node.visits) / child.visits)
score = exploit + explore
if score > best_score then:
best_score = score
best_child = child
return best_child
function Expand(node):
action = UntriedAction(node)
next_state, reward = SimulateAction(node.state, action)
child_node = CreateNode(state=next_state)
child_node.parent = node
node.children.append(child_node)
return child_node
function Simulate(state):
current_state = state
total_reward = 0
while not terminal(current_state) do:
action = RandomAction(current_state)
next_state, reward = SimulateAction(current_state, action)
total_reward += reward
current_state = next_state
return total_reward
function Backpropagate(node, reward):
while node is not None do:
node.visits += 1
node.total_reward += reward
node = node.parent
function BestAction(root_node):
best_action = None
best_value = -Infinity
for child in root_node.children do:
value = child.total_reward / child.visits
if value > best_value then:
best_value = value
best_action = child.action
return best_action
function SimulateAction(state, action):
# Simulate the effect of an action in the environment
next_state = TransitionFunction(state, action)
reward = RewardFunction(state, action, next_state)
return next_state, reward
function UntriedAction(node):
# Return an action that has not been tried yet from this node
# This function should consider the set of possible actions and filter out those already tried
return SomeUntriedAction(node.state)
function RandomAction(state):
# Return a random action from the set of possible actions for the given state
return SomeRandomAction(state)
function terminal(state):
# Determine if the state is a terminal state
return IsTerminalState(state)
五. 结论说明
我们尝试描述了一种基于马尔可夫决策过程(MDP)的动态定价模型,用于优化众包骑手的服务分配和定价策略。随着众包配送服务的快速增长,这种模型可能成为未来物流和配送系统的重要组成部分。该模型允许众包平台在为客户提供灵活且高效的配送服务的同时,最大化其收入。
为了解决我们的MDP模型,还尝试使用蒙特卡罗树搜索(MCTS)启发式算法来优化定价决策。在实际项目中还需要明确定价算法是否优于固定费率基线,并且在可以获得该基线的情况下,与最优价值迭代(VI)基线是否具有竞争力。
在一些别的定价项目中,会看到有同学采取因果推断的方式进行定价选择、价格补贴,这可能取决于我们的具体目标和问题特性。如果目标是动态地优化定价策略或资源分配策略,以便在不断变化的环境中最大化收益(如利润、效率或客户满意度),MDP是也是一个合适的选择。MDP可以帮助我们在不同状态下制定最优行动策略,并有效处理不确定性,通过概率模型预测不同状态的转移和相应的奖励。另一方面,如果我们希望理解某些因素(如定价策略、激励措施)对骑手行为或客户需求的因果影响,因果推断也可以作为补充加入。因果推断可以帮助识别哪些因素真正驱动了结果变化,并评估新策略的效果,尤其是在数据中存在混杂因素时,因果推断方法可以提供更准确的因果估计。
在后续项目中,结合两者的方法可能会更有效,例如,先使用因果推断识别关键因果关系,然后在MDP中利用这些关系进行优化决策。
参考来源:
【1】J. Gao, T. Wong, C. Wang, and J. Y. Yu, “A Price-Based Iterative
Double Auction for Charger Sharing Markets,” IEEE Transactions
on Intelligent Transportation Systems, vol. 23, no. 6, pp. 5116–5127,
Jun. 2022, issn: 1558-0016. doi: 10.1109/TITS.2020.3047984. [Online]. Available: https://ieeexplore.ieee.org/document/9325919
(visited on 08/09/2024)
【2】P. V. Dahiwale, Z. H. Rather, and I. Mitra, “A Comprehensive Review
of Smart Charging Strategies for Electric Vehicles and Way Forward,”
IEEE Transactions on Intelligent Transportation Systems, pp. 1–21,
2024, issn: 1558-0016. doi: 10.1109/TITS.2024.3365581. [Online].
Available: https://ieeexplore.ieee.org/document/10457989 (visited on 08/08/2024)











