用户体验设计部-交互设计组

史文超、韩玥颖

前言

客观指标监测是用户体验度量模型中的重要部分，而客观指标分布变换和指标基准值测定则是客观指标度量最重要的环节。正态分布函数的特性可以有效地辅助指标变换和基准值测定，本文将结合生产系统客观指标度量项目的实践经验，介绍正态分布函数在客观指标度量模型中的应用方法。

关键词

数据分析；体验度量；正态分布；分值计算；产品客观指标

背景描述

生产系统产品研发部门希望通过对其负责的生产系统客观指标度量推进产品负责制，监测重点产品指标的变化来评价产品经理推动落地的相关功能效果。因此本项目的工作主要分为两个环节：在生产系统重点功能模块埋点，取数并计算相应的客观指标数值；观察当期指标的变化趋势以及同指标长期变化的基准值进行对比，对当期的指标情况进行评价。

客观指标类型众多，结合不同的计算方法和统计口径更是纷繁复杂，客观指标的选择和计算是我们面对的第一个难题。产品研发部门基于自身需求考量，希望摒除用户线下行为的影响，只度量生产系统的运行情况。因此，客观指标的时长数据只包含：加载时长，操作响应时长以及少量包含操作的交互时长，再辅以访问情况、任务完成率和异常率、异常原因等指标数据，就构成了生产系统客观指标体系。限于篇幅，客观指标体系的构建过程不在此处赘述，后续会有相关文章进行总结复盘。

客观指标度量模型中的指标数据很多都是非正态分布。如去掉用户行为影响的响应时长类数据和传统的系统性能时长数据分布类似，都属于偏态分布。此类数据的核心特点是出现非常明显的拖尾，数据的均值计算出来之后，均值落在了图形的某一侧，偏离了主要数据集中的位置，导致均值对于群体而言已经没有代表性。对于此类指标以及更复杂的分段分布形式，可以通过多种变换工具将其转化为便于分析的正态分布或者近似正态分布的形式。

指标的正态分布变换

某个指标通过大数据平台取数后得到一组原始数据，原始数据呈现非正态分布的情况，此时在坚持正态性假设前提下，可以选择数据转换函数将非正态数据转换为正态数据；目前常用的几种正态分布转换方法包括对数变换、平方根变换、倒数变换、平方根反正弦变换和Box-Cox变换（又称幂变换），在使用时可以根据数据分布情况选择适当的变换方法。

为了后续简化叙述和公式格式统一，这里设原始数据为，转换后数据为。

1、对数变换

定义：将原始数据的对数作为新的分析数据，一般为了计算方便我们可以取自然对数（LN）和以10为底的对数（LOG10）。

公式：

• 如果数据全部大于0，则可选用或；
• 如果数据中有等于0，则可选用或；
• 如果数据中有负值，则可选用
• 或，其中，
• 或，其中。

适用范围：可用Excel函数处理计算原始数据的标准差（STDEV.S）、偏度（KURT）和峰度（SKEW）；如果数据是高度偏态（|偏度|>1）或者数据呈现明显指数分布、长尾分布，则通常可以采用对数变换。

2、平方根变换

定义：将原始数据的平方根作为新的分析数据

公式：

• 如果数据全部大于等于0，则可选用；
• 如果数据中有负值，则可选用
• ，其中，
• ，其中。

适用范围：如果数据满足泊松分布（方差与均数近似相等）或者是轻度偏态（0<|偏度|<0.5），则通常采用平方根变换（SQRT）。

3、倒数变换

定义：将原始数据的倒数作为新的分析数据 公式：

• 如果数据全部大于0，则可选用；
• 如果数据中有等于0，则可选用；
• 如果数据中有负值，则可选用
• ，其中，
• ，其中。

适用范围：常用于两端波动较大的情况，可使极端值的影响减小。

4、平方根反正弦变换

定义：先计算原始数据的平方根，然后取平方根的反正弦作为新的分析数据 公式：，其中

适用范围：常用于服从二项分布的比例或百分比、中度偏态（0.5<|偏度|<1）的数据。一般认为总体率较小（如＜30%）时或较大（如＞70%）时，偏离正态较为明显，通过样本率的平方根反正弦变换，可使资料接近正态分布，达到方差齐性的要求。使用时注意进行反正弦变换的数字必须在0到1的范围内，如果是百分比需先转化为小数后进行计算。

5、Box-Cox变换

定义：引入一个参数，通过数据本身估计该参数进而确定应采取的数据变换形式；本质上是上述4种变换的综合处理方式。

公式：

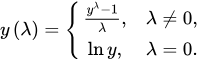
其中，为经Box-Cox变换后得到的新变量，是原始数据，是变换参数。其中原始数据y必须为正数，对于含有0或者负数的原始数据需要增加常数k，使得。

值不同时，可以得到不同的Box-Cox变换结果，当值为对数变换，当值为倒数变换，当值为平方根变换，其他常用取值如下图。

一般可以通过最大似然估计法来估计值，为了简便计算，我们可以借助Python实现Box-Cox转化:

• 首先求最佳值
• 然后根据最佳值进行Box-Cox变换

import pandas as pd
from scipy import stats
import sympy as sp

# 读取Excel文件
input_file = 'input.xlsx'
output_file = 'output.xlsx'
data = pd.read_excel(input_file)

# 判断是否需要增加常数K
min_value = data['Value'].min()
if min_value <= 0:
    constant_k = abs(min_value) + 1
    data['Value'] += constant_k
else:
    constant_k = 0

# 计算最佳Box-Cox的lambda值
transformed_data, best_lambda = stats.boxcox(data['Value'])

# 创建符号变量
x = sp.symbols('x')
y = sp.symbols('y')

# 定义Box-Cox转换公式
if best_lambda == 0:
    boxcox_formula = "y = log(x)"
else:
    boxcox_formula = f"y = (x^{best_lambda} - 1) / {best_lambda}"

# 输出Box-Cox转换公式和lambda值
print("使用的Box-Cox转换公式：")
print(boxcox_formula)

print("使用的Box-Cox转换函数：")
print(f"λ = {best_lambda}")

print("K值为：")
print(constant_k)

# 将转换后的数据写入新的Excel文件
data['Transformed_Value'] = transformed_data
data.to_excel(output_file, index=False)

从正态分布到评价分值的转化方法

通过上述的变换方法，我们可以得到一组指标数据的近似正态分布。而对于指标的评价是通过对比分析进行的。这里我们需要同一指标的两组数据：需要进行评价的当期数据组和作为比较基准的固定时段数据组（过往90天或180天）。此两组数据都是符合正态分布的，待评价数据组需要计算其算数平均值，基准数据组计算其算数平均值和标准差。

1、优化算数平均值的计算方法

通过埋点获取的初始数据会有各种异常，直接在原始数据基础上计算平均值，会导致计算结果失真，产生非常离谱的数据，因此在计算样本数据的算数平均值之前需要对数据进行处理，在计算算数平均值时，主要使用二次均化的方法，对原始数据进行处理。以响应时长指标数据为例，处理过程如下：

• 去掉样本数据中的负值；
• 去掉样本数据后5%的时长超长异常数据；
• 应用上述的变换方法，将样本数据转化为近似正态分布，基本分布形式如下：

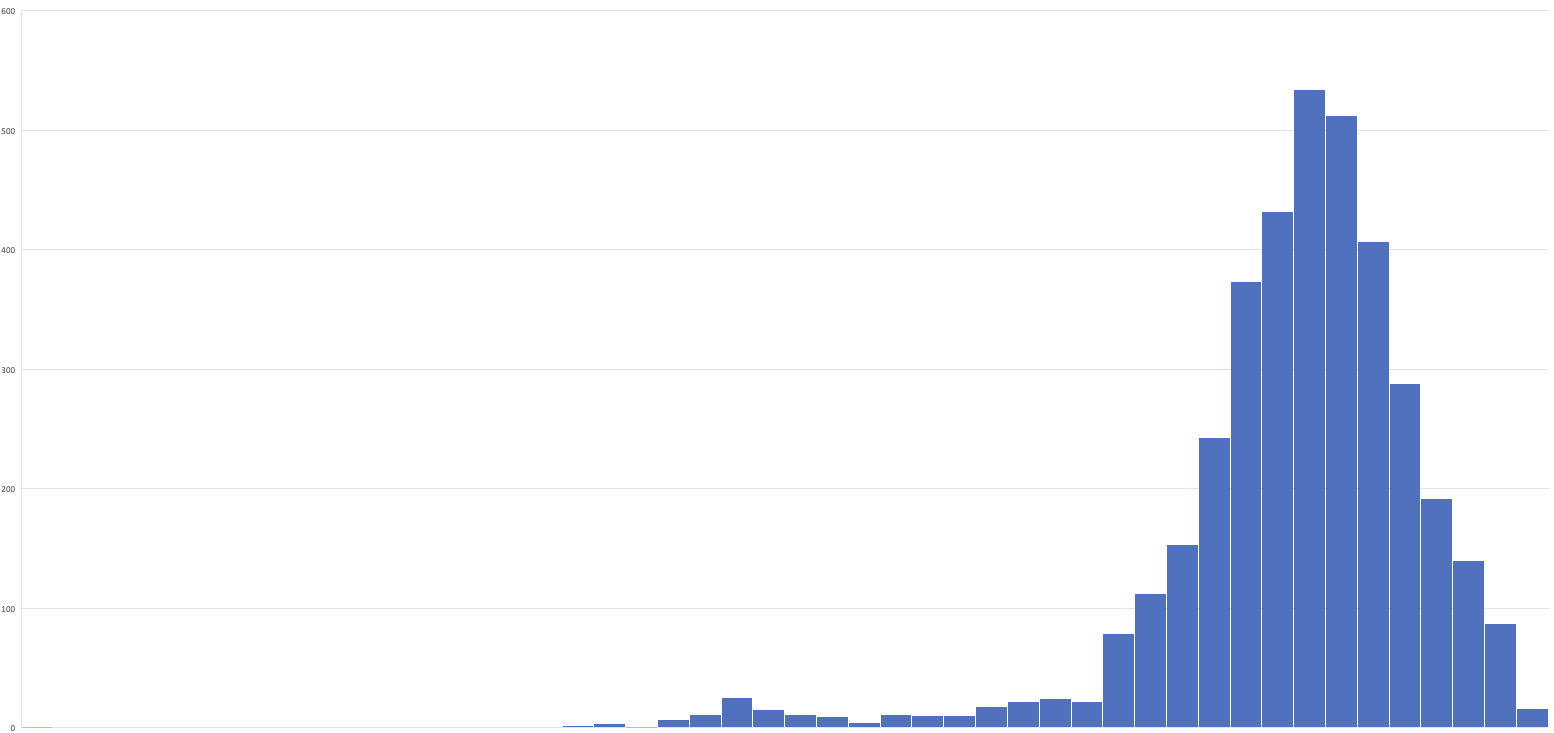
自动领取无需等待响应时长：近似正态分布

• 样本数据中去掉一个最小值、去掉一个最大值；
• 对待评价数据组计算其算数平均值，对基准数据组计算其算数平均值；
• 将计算得出的算数平均值和，重新置入转换后的正态分布中考察其所处的位置，如果偏左则与分布的60%分位处的数据加和求平均值，如果偏右则与分布的40%分位出的数据加和求平均值，计算得出二次均化后的算数平均值和；
• 计算基准数据组的标准差。

完成上述步骤的数据处理后，后续工作需要的参数计算完成。

2、基准数据组和总体分布之间的偏差处理

由于指标的总体分布是无法完全测量的，所以我们要通过基准数据组去拟合总体分布情况。理所当然的，基准数据组的算数平均值和标准差与总体会存在偏差。为了更好的反映总体情况，我们可以通过抽样平均误差和标准误两个指标来衡量样本和总体之间的偏差情况。在本次项目中受数据量影响暂时没有处理样本和总体的偏差问题，因此也没有实践经验分享，有兴趣的同学可以通过这两个指标进一步查阅相关的资料。

简而言之，我们可以通过增加抽样的次数以及单次抽样的样本数量来降低样本和全集总体之间的偏差。在实际操作过程中，如果样本数量低于200，样本可能无法通过正态分布检验。样本数量在400以上时，较容易通过正态分布检验。这样的经验值希望能够对大家有用。

3、正态分布累积概率到基准值的转换

通过上述的变换方法得到的正态分布都不是标准的正态分布，两者之间需要一个简单的转换。标准正态分布原值和普通正态分布值的关系为：

进一步考虑如何通过这个数据分布形式来将数据转换成得分和数值，这里需要将正态分布的累积分布函数（误差形式）写出来：

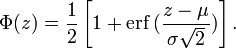
通过以上两个公式，可以获得原值和其对应的累积概率之间的关系。考虑到已知累积概率，求解原值比较困难，早已经有标准正态分布的值表，供我们查阅使用：

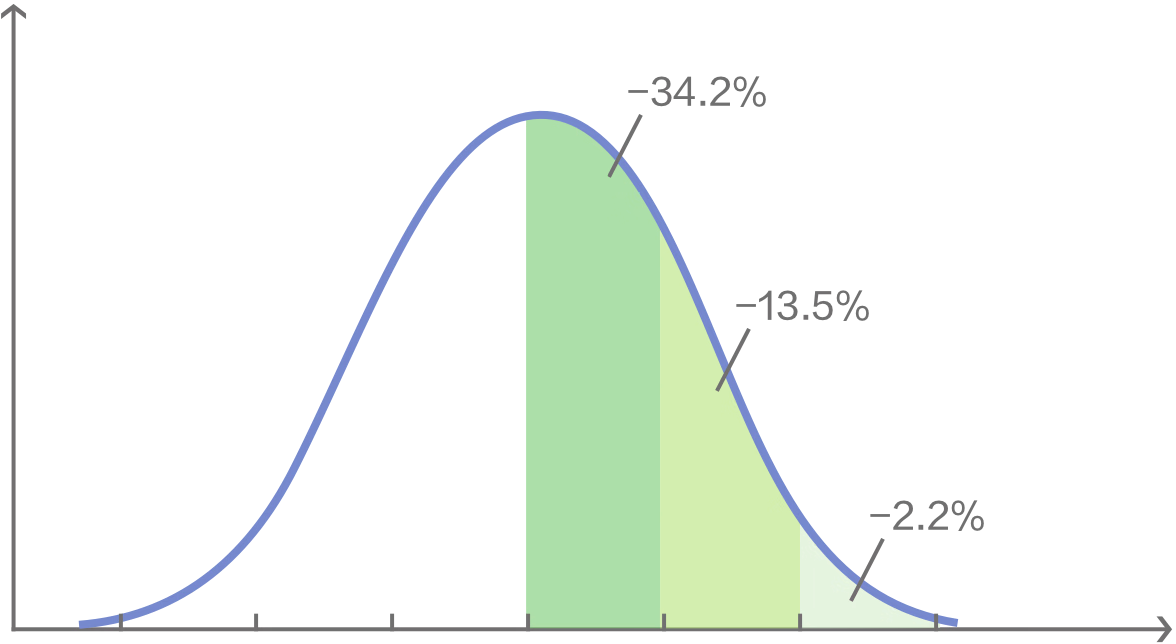
左单侧对照表：

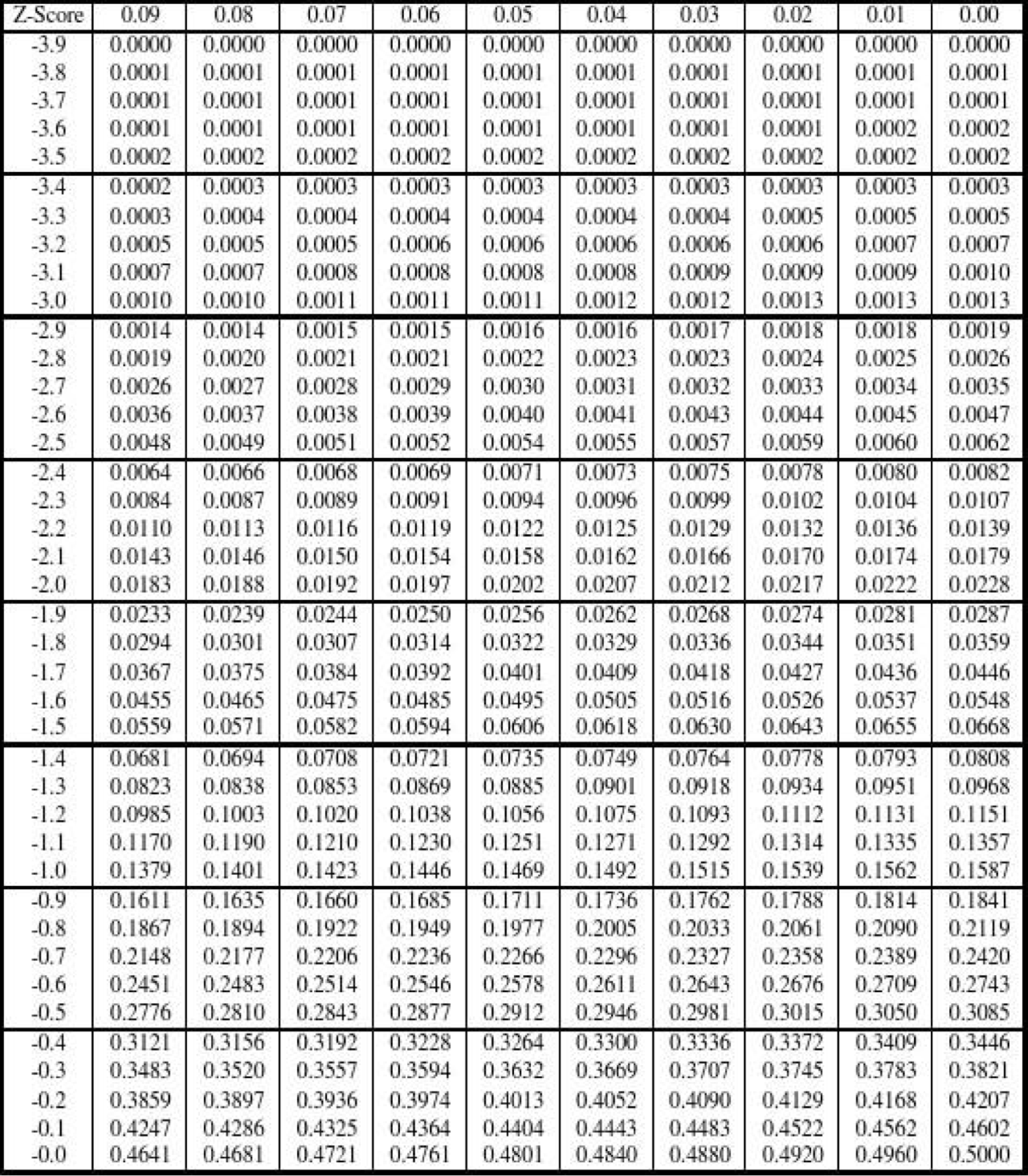
右单侧对照表：

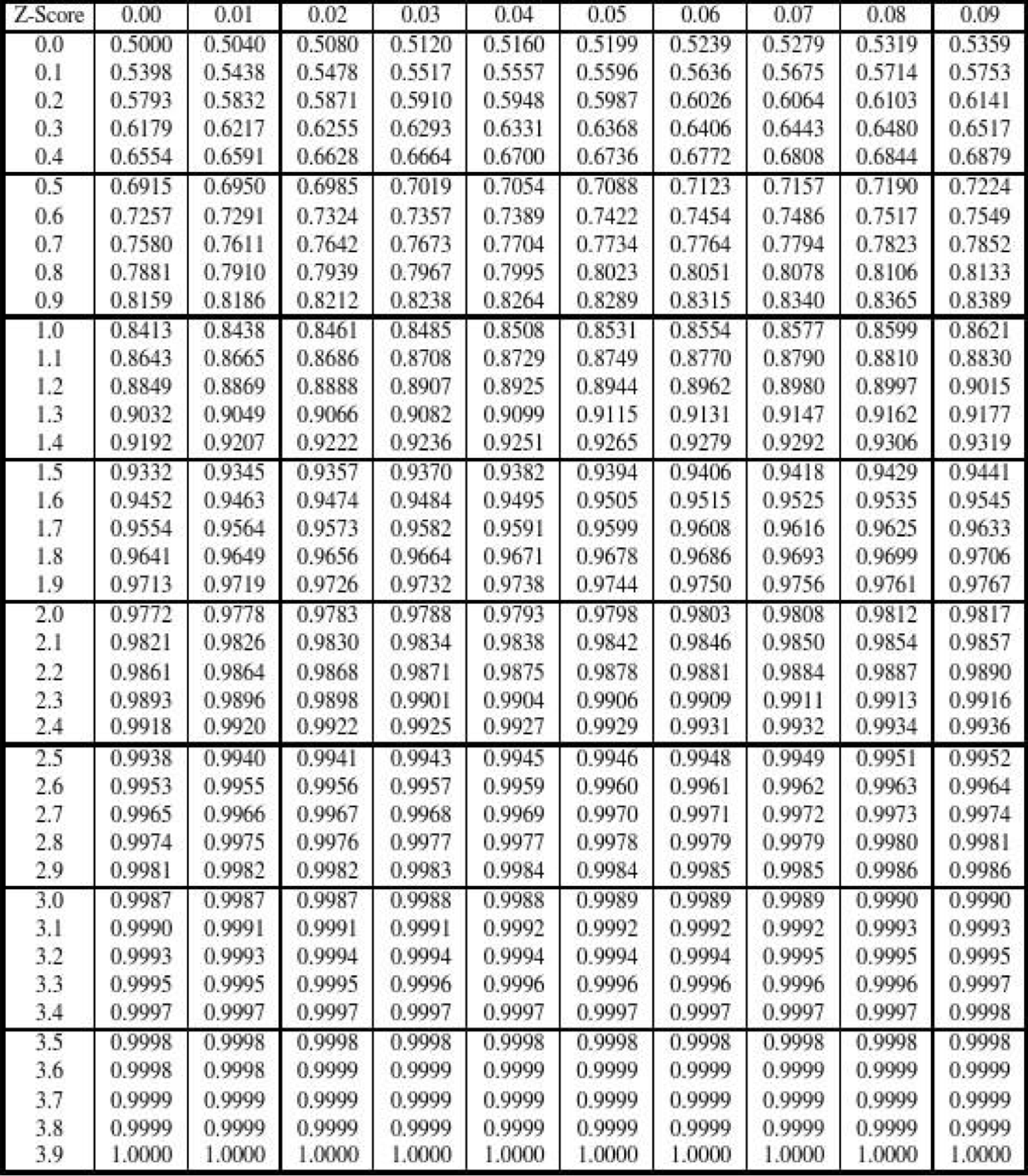
上述的求解过程可能不容易理解，我们在这里可以举例说明：现有某个提交按钮的响应时长数据，已经处理为近似正态分布，计算出其算数平均值= 5.378，标准差= 1.023，希望计算其累积概率为40%时对应的指标值。查阅上述表格可知：= 0.4时的值为-0.25，简单列一下已知的数据：

变换一下指标值和原值之间的关系为：

代入各参数值，可得指标值为5.122。

对于加载时长，其值是越短越好。因此对于上述计算结果的解释为：如果待评价的当期指标均值小于5.122秒，则当期指标表现在指标整体表现中处于前40%的位置，即当前指标表现超过了指标整体60%的情况。如果按照百分制，当前表现已经超过了及格线（60分）。

通过上述计算方法得出的指标值即可以作为指标的基准值使用。我们还可以通过代入不同累计概率值，计算不同分位的指标基准值。

4、关于评价分值的一些想法

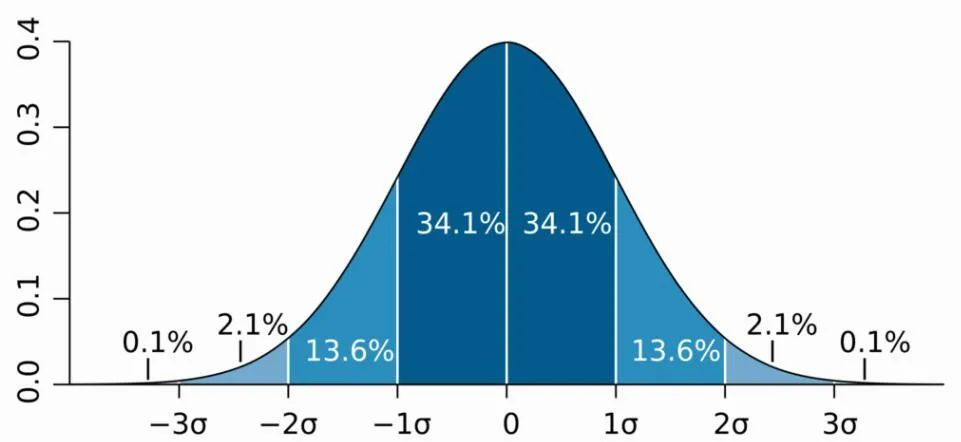
经过一段时间用户体验度量模型的实践，对于客观指标赋分的方法有一些探索和总结。其核心都是以指标正态分布为基础，对其波动范围进行划分，进而赋分。方法主要为分箱法和区间映射法。下面简述两种方法的区别：

分箱法

简而言之，通常是以标准差为刻度，对指标分布的范围进行划分，还是以加载时长举例：以下为5分，到之间为4分，到之间为3分，到之间为2分，到之间为1分，以上为0分。

分箱的方式可以有很多种，上述提到的测定基准值的方法本质上也是一种分箱，即指标低于基准值是好，高于基准值就是差。分箱法的优势是简洁直观，缺点是分箱通常比较粗犷，分值不敏感，难以进行定量分析。

区间映射法

区间映射法的本质是将指标波动的范围和分值区间进行映射，在快递小程序的体验度量模型中，度量值的赋分区间划定如下：

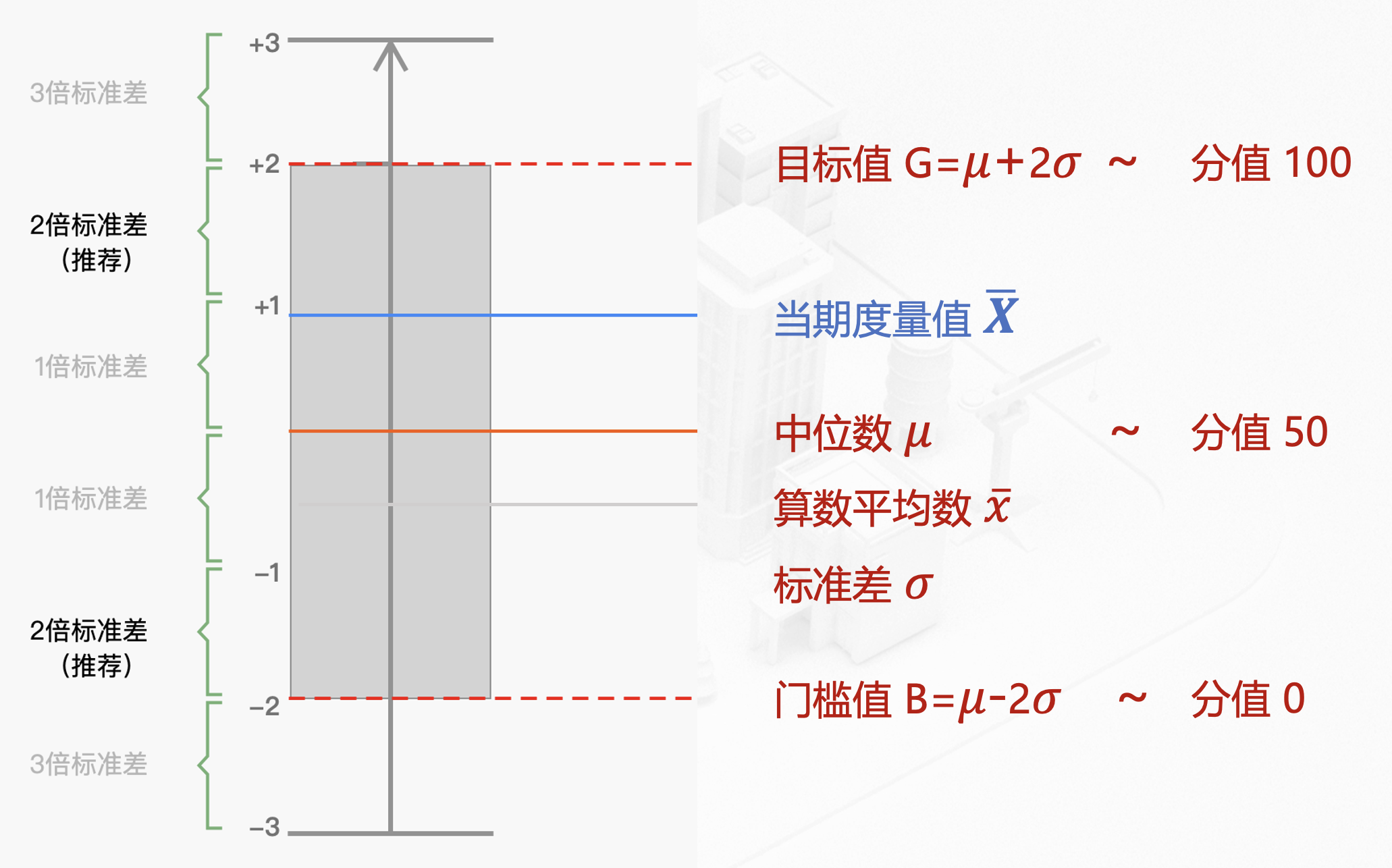
在实际应用中我们发现，由于样本数据和总体数据分布的偏差，特殊情况下，会有实际度量值超过目标值或者低于门槛值的问题，进而导致分数极值，失去度量意义。通常后续会增加限制条件来处理指标极值问题。这种赋分方式适合之前已经有过度量工作，后续增加客观指标部分的情况。这种方式通常可以设定底分，保证度量模型平稳过渡。

在上方章节提到的通过特定的累积概率求对应指标值的方法也可以转化为一种区间映射的赋分方法。即通过值表，获得累积概率为0%～100%区间对应的指标值的范围，设定累积概率为0%时的指标值为100分，累积概率为100%时的指标值为0分。用待评价的当期指标均值和指标值范围去比较，直接转化为相应的分数。

这种赋分方法的优点是永远不会出现超出指标范围的特殊情况，其缺点则是由于指标范围较大，可能导致分值不敏感，分数波动小。初始分数可能会很低，只适用于最初就使用此种赋分方法的情况。

这种将累积概率直接转化为评价分值的方法只是在项目过程中探索发现的一种想法，目前并没有实际应用到度量模型中接受实践的检验。在此表述出来也希望能够对各位读者有所启发，也欢迎将其应用到实际项目中试验，分享试验结果。

正态分布数据变换的局限性与解决方法思考

在处理数据的过程中，正态分布变换只是为了方便数据分析的一种方式，并非所有数据变换完成后都能服从正态分布，比如离散型随机变量分布、多峰分布等。本文中阐述的正态分布转换方法经过检验后更适用于时长类的指标分析，对于率值类的指标（比如成功率、失败率）存在一定的局限性，需要根据实际情况选择更适合的分析工具和方法。

一般情况下，如果通过变量转换的方法依然无法将数据转化为正态分布的话，可以考虑采用分段分析或者非参数检验的方法来进行统计分析。

1、分段分析

如果数据呈现明显的多段特征时（比如缺口多、数据分布形态有明显分界线），可以考虑将数据切分为多段分别处理和分析。

例如在本次关于失败率的指标分析时，发现指标经过平方根变换后仍存在明显二段特征，第一段数据均为常数0，第二段数据符合近似正态分布；那么结合实际经验认知，失败率为0的情况可以单独归结到数据集1中单独处理，失败率非0的数据可以归结到数据集2中进行单独处理。

如果需要进一步对多段数据取基准值进行评价赋分时，可以考虑在每个数据集单独按照文中阐述的40%分位基准值测定方式求出子基准值，后续按照数据集占比作为权重，求子基准值的加权平均值，次方法可以用于粗估多段数据的基准值，后续可以结合专家经验得出经验值进行修正。

2、非参数校验方法

例如Wilcoxon检验和Mann-Whitney U检验方法等，本次由于文章篇幅暂不对此类方法进行详细说明。

附录

正态分布变换参考内容链接：

http://www.biostathandbook.com/transformation.html

https://wenku.baidu.com/view/96140c8376a20029bd642de3.html?_wkts_=1695650860214