★ halo,大家好~很开心又和大家见面了~
★ 在第一篇 楠姐技术漫画:图计算的那些事 发布之后,楠姐收到了很多建议、鼓励和支持,非常感谢大家的喜欢,所以楠姐尽自己所能马不停蹄开始第二篇的创作,虽迟但到~
★ 本篇依然是风控算法分享,其实也依然算是图算法系列。社区发现作为最基础的图算法之一,也是楠姐在2020年入职后,第一个跟着大腿有样学样,学习、上手和应用的图算法,因此在第一期之后,楠姐就立刻决定把它单独拿出来写一期~~进一步来说,无论图计算今天和日后发展如何,我们都不该忘记最初的前人基石,同时也希望自己和每个小伙伴,无论路已走多远,都能不忘初心,不忘滴水之恩。

--- ★ PART 1 ★---
其实社区发现
也并不是什么难懂的名词
相信所有看过第一期漫话的宝子们
应该还没忘记图的概念
那社区又是什么呢?

社区其实反映的是
网络中的个体行为的局部性特征
以及其相互之间的关联关系
换通俗一些的说法...

用户之间的点赞、私信、关注等动作形成了边
那些关联尤为紧密的用户就形成一个社区
而分属不同社区的用户之间
关联则非常稀疏或根本不存在关联
近几年流行的饭圈文化就是一个很好的例子

明白了什么是社区
其实社区发现所要做的事也就很易懂了
正是要发现这些潜在的、有特定关系的节点集合
以及每个社区中都有哪些节点
这样做的目的和效果也有很多

我们京东的注册/营销/支付/物流/信贷等各大系统
黑产团伙在很多细节上的关联总是非常紧密的
与正常用户显得格格不入

再比如生物学领域内
基因调控网络分析、主控基因识别
还有疾病传播学中
传染关键社区识别以及易感人群发现等

还有上一期评论区中提到的
👍基于社交网络的海王识别器👍
都可以用到社区划分

一是要确认当前使用场景内
确实存在着明显聚集规律
节点间存在一定的逻辑可以形成社区结构
而不是无规律分散

二是不要把社区拓扑结构与欧式空间结构混淆
虽然在欧式空间中
向量夹角小的点向量彼此距离近
向量夹角大的点向量彼此距离远
但即使距离相近的点向量
也不一定就存在业务或者逻辑上的拓扑关联

牢记以上两点
才不会让你的社区划分被限制使用方式或失效
--- ★ PART 2 ★---
那说到这呢
可能会有算法的小伙伴发现
社区发现好像和聚类非常相似
它们都属于无监督算法
聚类要做的是
“簇内距离最小化,簇间距离最大化”
社区发现要做的是
“社区内部节点关联紧密,社区之间节点关联稀疏”
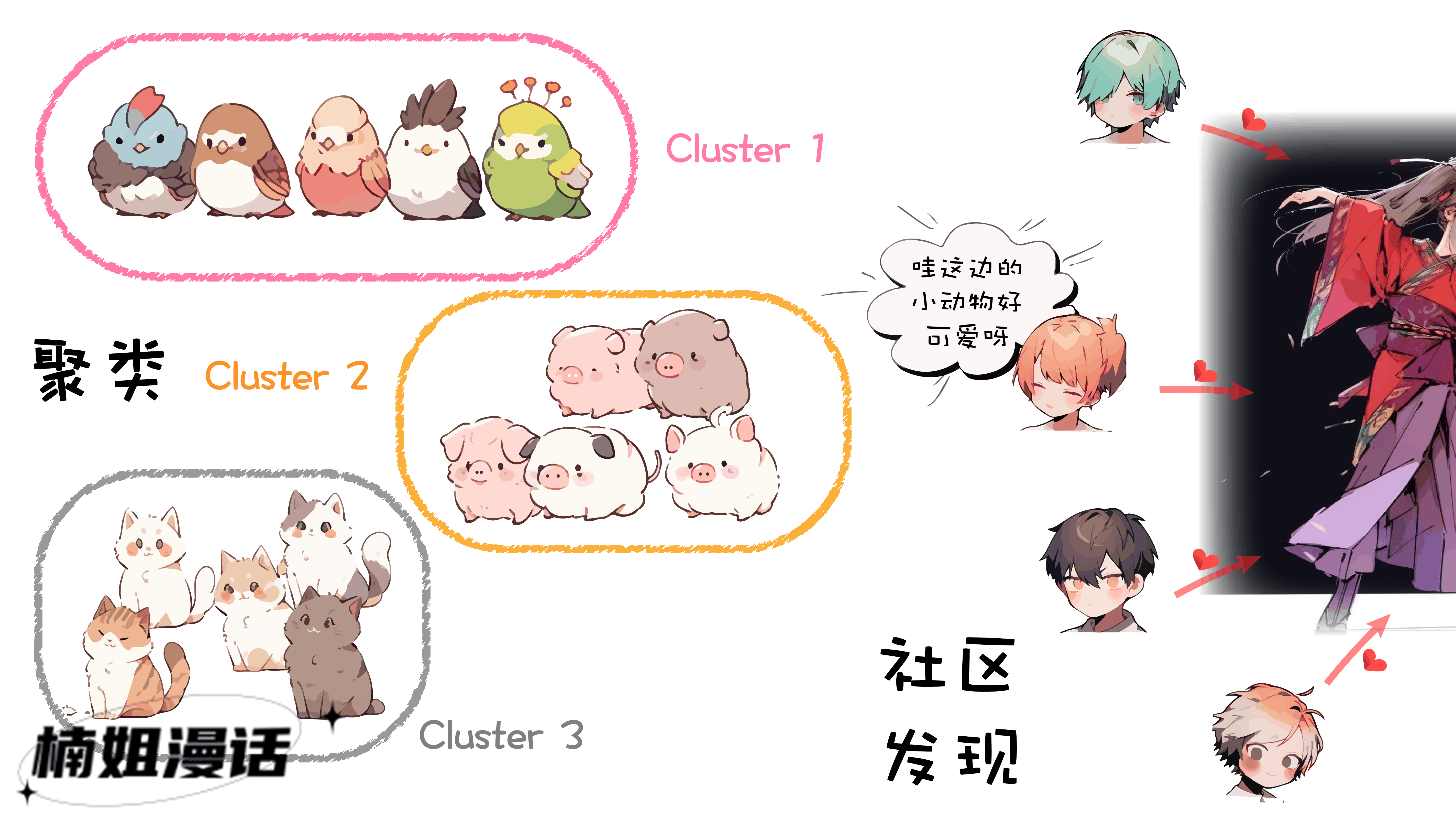
确实二者之间存在着很多相似性
但依然也是有区别的
机器学习中常见的聚类算法
本质上是一种更通用的方法
适用于多种常见的数据类型
而社区发现本质上则是图结构上的聚类
而关于社区本身
其实也有两种不同的类型
非重叠社区和重叠社区
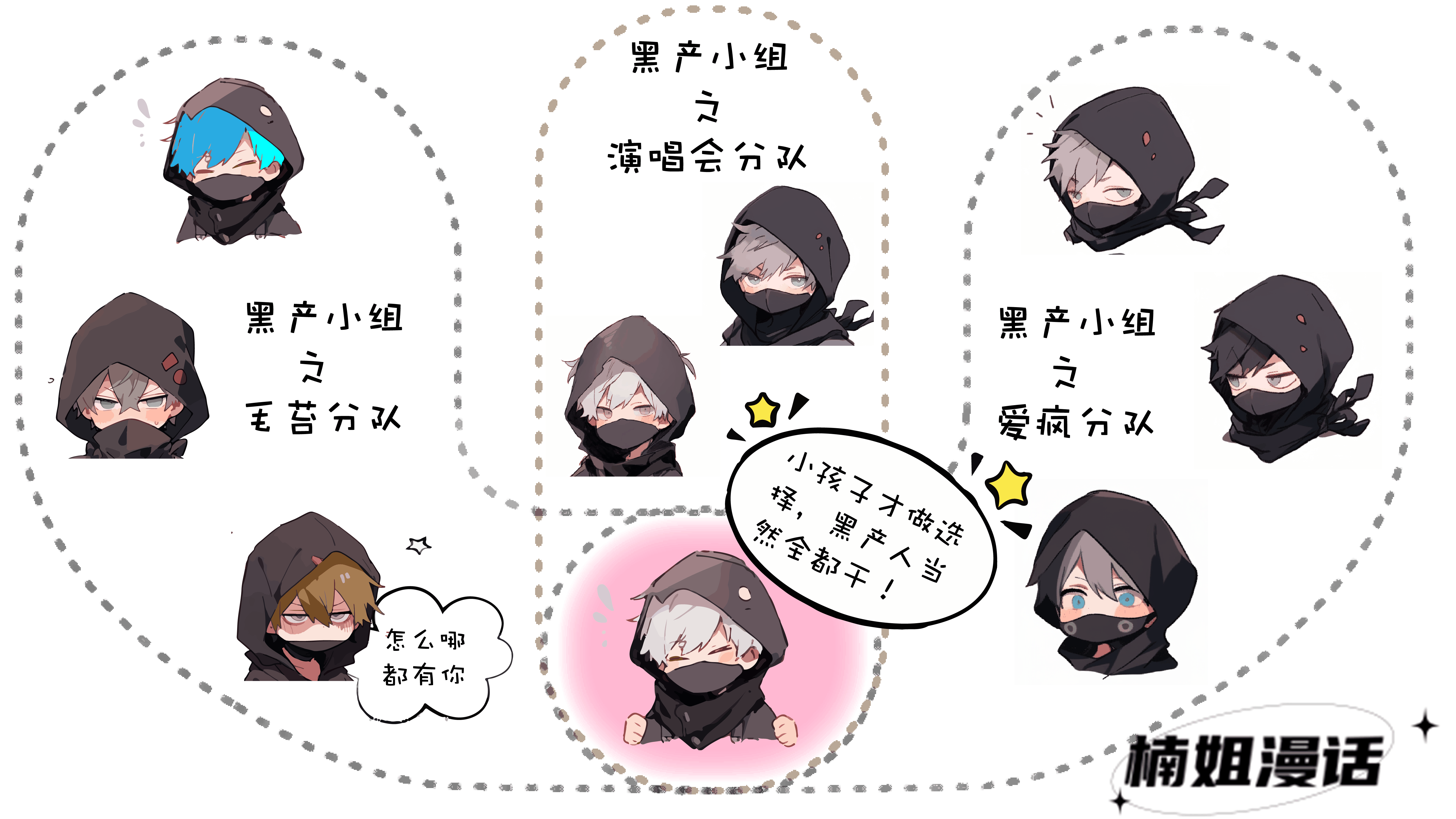
前者说的是图中的每个节点只属于一个社区
而后者则允许同一个节点可以分属于多个社区

--- ★ PART 3 ★---
社区发现算法类别繁多
不同算法划分的社区自然也是不同的
不管是人还是模型去执行一些学习任务
都有关于学习是否到位的评判方法

那我们如何评价一个社区发现算法的好坏呢?
此时就不得不先提一个重要的基本概念
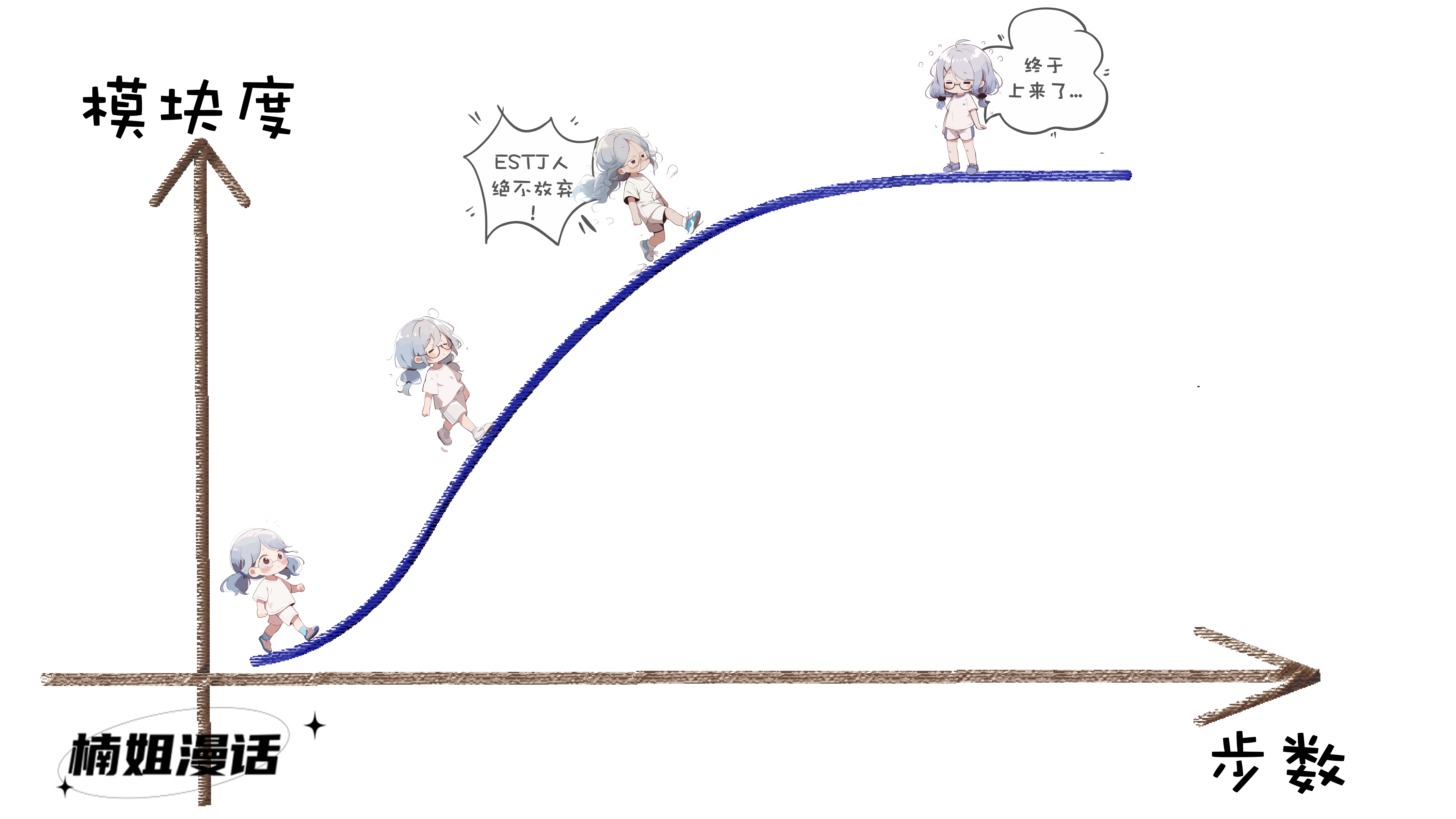
模块度(modularity)
这是一种常用的社区划分评估指标
为了怕大家睡着从而忘记一键三连
楠姐贴一个简化版的模块度计算公式
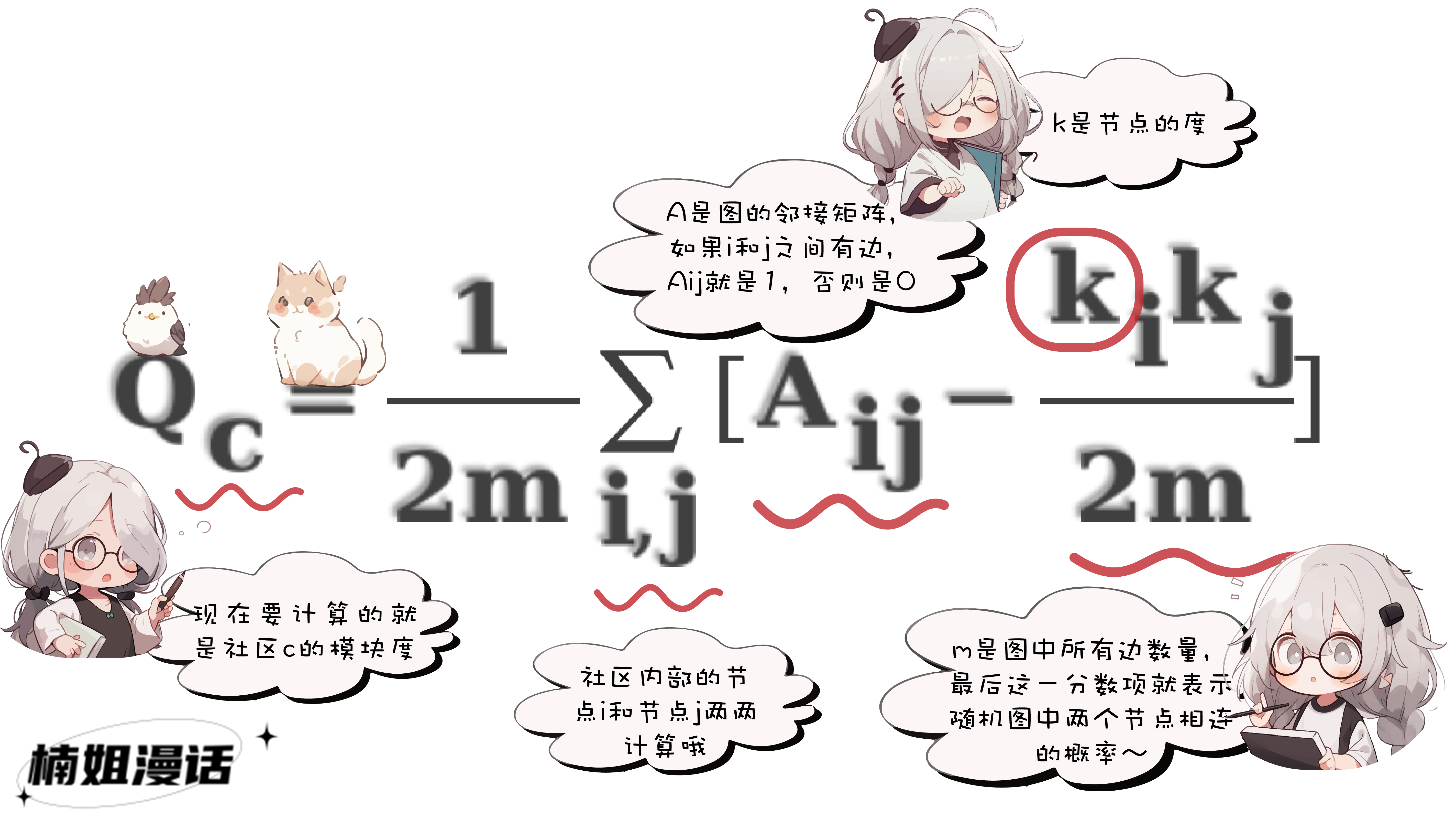
通俗来说
模块度的物理含义是
社区内部的边数与随机情况下的边数的差距
如果越大,说明社区内部密集度高于随机情况
这里的随机情况指的是图中节点和边的数量不变
把节点之间连接关系随机打乱
一个图如果看起来不像随机产生的
那可能就是存在社区的

如果一个社区发现算法
尽可能多的将关联紧密的点划分在同一社区中
尽量避免所得社区之间还存在过多的边
这样就能得到较高的模块度
也会被认为是较好的一种划分方式
--- ★ PART 4 ★---
自从2002年“社区”概念被提出后
社区发现算法就一直在快速发展

★
首先是比较直接的基于模块度的社区发现
这类算法直接把模块度作为优化目标
有着良好的解释性
Louvain算法是其中的典型代表
它的二阶段思路非常清晰

第一个阶段称为模块度优化阶段
先把图中的每个节点都视作一个独立的社区
对每个节点
依次尝试将其分配到它每个邻居节点的社区中
计算分配前后模块度的变化
并将该节点分配至模块度增益最大的一个邻居社区中
如果没有任何一个邻居社区能提升模块度
则该节点的社区保持不变
对所有节点进行一轮以上计算后
一些节点便已经被划分在了同一个社区
接着开始第二阶段——社区聚合阶段
把同一个社区的节点视作一个新的节点
社区内部的边视作权重和累加的自环边
社区之间的边视作新节点之间的边
根据这个新的图结构再重复第一阶段
两个阶段循环往复
直到模块度不再更优为止
Louvain算法由于其较低的时间复杂度
十分适用于大规模网络的社区检测
也成为应用最广泛的算法之一

★★
第二种经典方法
是基于节点表达的社区发现
该类方法将图节点表达和映射到多维向量空间
并结合传统聚类算法将它们聚集成社区
这种方法不可避免的要进行矩阵计算
或者使用额外的节点表征算法
计算开销很大
但它能直接使用传统聚类的成果
因此灵活性非常好
比如,典型的一个方案就是
使用node2vec进行图节点编码
再使用聚类将相似的节点向量进行聚合

node2vec其实是借鉴了NLP领域中的word2vec
简单来讲,它先会在图结构中进行随机游走
通过随机游走
采样出多条节点序列
类似于文本序列
而我们要表征的节点
就类似于文本中的字词
再使用NLP领域中常用的SkipGram算法
将节点表示成量化的向量表达

以文本理解为例
如果我们想让人工智(zhi)能(zhang)理解下面这句话:

那是不是可以把这句话中“技术漫话”遮挡住
让模型进行填空:
“楠姐发了____,很快就要火了”
如果模型能正确填上
就可以一定程度代表模型学会了这句话中每个字词的含义

或者反过来也可以
把除了“技术漫话”之外其他的字全部遮挡住
让模型进行补写:
“____技术漫话,_________”
要是模型补充的很不错
也代表模型学会了这句话和里面的字词

上面做的这些事
就是NLP领域内的word2vec算法
第一种填空的方式叫CBOW模型
第二种补充的方式就是SkipGram模型
在图的节点表征中
用于图节点序列也是一样的道理

那么说回社区发现
有了节点的数值表示
就可以借助任意一个传统的聚类算法
达成最终的节点社区划分的目标
但是分两步的方法终究费时费力
也有一些优秀的算法
可以将节点编码和聚类合二为一
一起进行优化

单纯是由于懒
楠姐就不再赘述
★★★
今天要说的第三种经典的社区发现思路
是基于信息论的社区发现
里面的典型代表是楠姐的“老熟人”
——赫赫有名的infomap算法
它也采用了在图中随机游走的方式进行节点序列的采样
但它社区发现的目标
是最小化节点的平均编码长度

所谓编码
其实就是用有限个标记的组合来表示原始信息
大家最熟知的就是二进制编码
即只用0和1两个数字
编码与原始对象通常是一一对应的
比如“楠”可能对应着“11”,“姐”对应着“1001”,那么“楠姐”就对应着(11,1001)

如果需要我们快速地记录下所看到的文字
记录的方式需要将每个字对应一个二进制编码
那为了记得更快
我们显然是希望经常出现的字用短的编码
比如“楠姐”这个词如果出现的很频繁

如果用“11000010001”来表示“楠姐”
要是每次听到“楠姐”都需要写这么长的数字
该是多么一件糟心的事情

如果用短的编码,比如“10”来表示“楠姐”
那相对而言记录速度就能有明显提升
也显得“楠姐”没有那么讨厌了
那么该如何找到一种最优的节点编码
使得平均编码最短呢
这个在信息论中已经给出了严谨的公式计算
也就是存在着一个“信息熵”的极限

不管用什么样的编码方式
其平均编码都不可能低于信息熵
这个信息熵也正是无损压缩的能力极限
这也正是信息论中的最小熵原理
回到Infomap算法本身
它额外借助了一个分组编码的思路
把最小信息熵和社区发现结合了起来

有没有一种可能
大家选择的记忆方式是酱紫的:
前面五个是人类活动
其次两个是搬砖项目
再往后三个是好吃的
后面三个是游戏
最后大家再分别记住四种分组里具体都有什么

是的,没错
这样的记忆方式就是一种更高效的方式
也是infomap所采用的编码方式——层次编码
它把每个节点都尝试进行分类
节点的编码均为在类内的编码
额外还有一套独立的类别编码
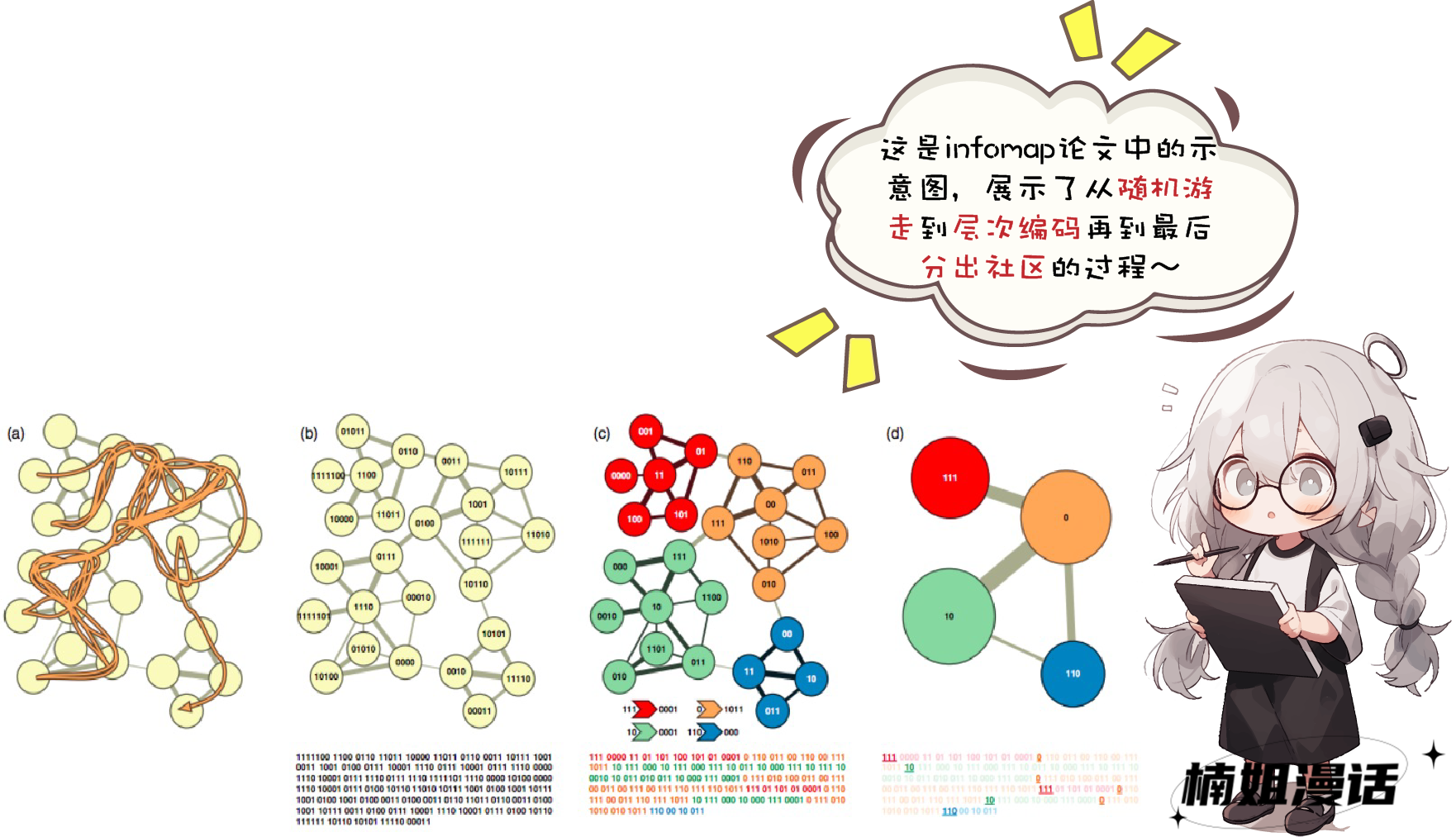
由于有了分类的思想
不同类的节点可以使用相同的编码
比如“楠姐”和“东坡肘子”都可以用使用“01”
这样就无形中压缩了整体的编码长度

再加上前面提到的最小熵目标
我们就可以搜寻一种最优的分层编码
来使得最短平均编码长度越小越好
最后每个节点编码时的分类
就是最终所属的社区
Infomap最大的优点也在于此

真是一种强大且漂亮的算法
还有一些其他类型的社区发现
比如基于标签传播的方法
基于图分割的方法
广义社区发现等等
感兴趣的宝子们可以卷起来了!

--- ★ PART 5 ★---
社区发现算法算是图计算中的一条重要分支
也是我们风控技术中离不开的工具
它在纷繁复杂的网络结构中
总能提供给我们一种微观视角
揭示着事物的结构和本质

只要你的想象力足够丰富
就绝对有社区发现算法所能发挥的空间
事在人为,行则终至!
加油吧,算法攻城狮们~

----写在最后----
★ 本篇文章图片构思、创意、整体结构、后期修改,全部版权归楠姐所有,素材生成均源自于Midjourney以及楠姐原创提示词生成。楠姐出图不易,并非完美,请勿未经允许用于其他场合及目的。
★ 本篇文章图片创意均只为了说明及示意,且带有一定夸张和幽默元素,切勿对号入座哦~如有雷同,纯属巧合~无意冒犯~
★ 本篇文章文字均根据以下参考文献汇总撰写:
[1]. 马耀,汤继良. 图深度学习[M].电子工业出版社.
[2]. 张长水,唐杰,邱锡鹏[M]. 图神经网络导论[M].人民邮电出版社.
[3]. CSDN. 写综述想到的[EB/OL]. https://blog.csdn.net/loptimistic/article/details/8173555
[4]. CSDN. 社区发现(Community Detection)算法[EB/OL]. https://blog.csdn.net/huangxia73/article/details/11801661
[5]. 博客园. 社区发现算法总结[EB/OL]. https://www.cnblogs.com/nolonely/p/6262508.html
[6]. 知乎. 简析社区发现和聚类[EB/OL]. https://zhuanlan.zhihu.com/p/428821516
[7]. 知乎. 万物皆网络,万字长文详解社区发现算法Louvain[EB/OL]. https://zhuanlan.zhihu.com/p/556291759
[8]. CSDN. infomap最全面易懂的解释--最小熵原理:“层层递进”之社区发现与聚类[EB/OL]. https://blog.csdn.net/jinking01/article/details/103511553
★ 楠姐技术漫画由于制作成本高,耗时长,因此可能不一定会在神灯上持续更新~也欢迎关注个人微信公众号“楠姐漫话”~楠姐只要有条件,一定坚持创作~感谢每个小伙伴的支持和厚爱!












