解读论文：When Homomorphic Encryption Marries Secret Sharing: Secure Large-Scale Sparse Logistic Regression and Applications in Risk Control【1】

引言

之前的纵向联邦逻辑回归模型 (Hetero LR) 多是基于同态加密或秘密分享，而近几年有几篇将同态加密 (HE) 与秘密分享 (SS) 技术结合的文章。本篇论文【1】介绍了隐语开源的可信隐私计算框架的纵向逻辑回归模型原理，就是应用了同态加密结合秘密分享技术，而FATE非中心化的纵向逻辑回归的实现也是在此篇论文的基础上进行了部分的优化。以下的主要内容介绍了该论文的技术要点及方案，并在最后对比了一下该方案与论文【6】中关于纵向逻辑回归模型方案的区别。

摘要

逻辑回归 (LR) 是业界最常用的模型，由于数据隔离问题及数据安全法、个人隐私保护法等法律法规的出台，业界合作建模需要一种更加安全高效的多方纵向逻辑回归模型。之前通常的解决方案有基于同态加密 (HE) 或基于MPC中的秘密分享 (SS) 的纵向逻辑回归。其中，以同态加密为基础的模型具有较好的通讯效率处理高纬稀疏特征，但是在模型训练过程中会泄露多余的信息，有安全风险。而秘密分享为基础的模型则被证明具有较强的安全性和较好的计算效率，但是他们不能处理高纬稀疏特征。因此，本文介绍了一种结合同态加密 (HE) 与秘密分享 (SS) 技术，可以保证安全性且具备处理高纬稀疏特征的纵向逻辑回归模型 (CAESAR)。实验显示CAESAR的性能比当时最先进的安全模型提高了约130倍。

1 简介

基于同态加密的Hetero LR模型问题：以同态加密为基础的模型分为中心化和非中心化两种。中心化模型的数据可能会被中心端滥用，既而增加了潜在信息泄漏的危险。而非中心化模型会在模型训练阶段将部分模型信息以明文的形式暴露给服务端或其他参与方，这部分信息可能推导出其他隐私信息，即使在半诚实安全假设下，这类型模型无法被证明是安全的。

基于秘密分享的Hetero LR模型问题：很多大企业提出了基于多方安全计算 (MPC) 中秘密分享协议的安全机器学习算法方案，相关的安全隐私保护机器学习框架有Facebook开源的CrypTen，Visa发展的ABY。与同态加密 (HE) 为基础的模型相比，秘密分享 (SS) 有被证明具有较强的安全性，但是它不能高效的处理稀疏特征，并在大数据量的时候，具有极高的通讯复杂度。

1.1 研究与实践的差距

（1）参与者的数量
在之前大部分的研究中，任意数量的参与者都可以联合建模，但在实际应用中，通常是两方共建模型。这是因为当涉及更多的参与方时，也会涉及到更多商业利益及法规。

（2）数据划分
大部分的研究会同时适用于数据纵向划分和数据横向划分两种情况，但在实际应用中，当参与方为大公司时，通常他们有相同的样本但不同的特征，即数据纵向划分。目前，只有少量研究专注于这种特定的情况并发挥这个情况的特点。

（3）特征稀疏
之前的研究忽略了现实情况下由于特征值缺失或经历过特征工程的处理，如one-hot编码，特征是高纬度且稀疏的。因此，如何搭建安全的高纬稀疏逻辑回归模型在数据纵向划分的情况下对于工业应用是一个具有挑战性的、有价值的课题。

1.2 本文的贡献

（1）一种新的结合同态加密 (HE)与秘密分享 (SS) 技术的协议 (CAESAR)。保证了安全性且兼具高效处理高纬稀疏特征的能力。

（2）分布式框架的实现。保证了本文的实现可以拓展到大规模数据集。

（3）现实生活中的部署和应用。将CAESAR部署到实际风险控制项目里，实验结果表明CAESAR显著的优于当前最先进的安全模型SecureML【2】。在特定环境下，与SecureML【2】相比，CAESAR有130倍的加速。CAESAR也是第一个可以高效处理大数据集的安全逻辑回归模型。

2 基础知识扫盲

2.1 两方数据纵向切分

根据参与方们的数据特性，分为两种不同的情况。横向数据切分指的是每一方拥有相同的特征和不同的样本，纵向数据切分意味着每方有相同的样本和不同的特征。本文专注于纵向数据切分的情况，在现实中，合作方会在第一步进行隐私集合求交得到两方数据的交集，再进行建模。

2.2 威胁模型

本文考虑的是标准的半诚实模型，即某参与方会在遵循协议的前提下通过分析自己得到的信息尽可能尝试获取另一方的输入。

2.3 秘密分享

2.4 加法同态加密

加法同态加密方法，例如OU、Paillier，广泛地被应用于机器学习模型算法，使用加法同态加密通常有以下几个步骤。

• 密钥生成：生成一对密钥对，公钥和私钥，将公钥发送给其他参与方。
• 加密：使用公钥和随机数加密明文数据。
• 同态运算：将明文 x、y 加密得到密文 [[x]]、[[y]] 。这里有三种运算方式。

(1) [[x+y]]=x+[[y]]

(2) [[x+y]]=[[x]]+[[y]]

(3) [[x · y]] =x · [[y]]

• 解密：将密文 [[x]] 解密得到明文 x 。

2.5 逻辑回归模型

• 建模与损失计算逻辑回归的目标是训练一个模型 w 使得损失函数最小。损失函数的公式如下:
• 小批次梯度下降

逻辑回归模型可以使用小批次梯度下降最小化损失函数来达到高效的学习。在每一次迭代中，选择一批次的样本，通过当前批次平均样本偏导数来更新模型。当 B 为当前批次的样本，|B| 为当前批次的样本大小，X_B 和 Y_B 是当前批次样本的特征和标签，是控制步长的学习率，模型更新表达式如下：

注：此公式为了简略省去了正则项。可以观察到在更新模型时涉及到了矩阵乘法，现实应用中，特征通常是高纬稀疏的，因此稀疏矩阵的乘法是处理大数据机器学习模型的关键。

• Sigmoid函数近似

在逻辑回归模型中的非线性sigmoid函数是很难加密计算的，因此，当前的研究提出了许多不同的渐近方法。例如Taylor展开、Minimax Approximation、Global Approximation、以及Piece-wise Approximation。在对比了这些方法在多项式阶数为3时的近似结果，本文选择了最佳表现的Minimax Approximation。根据论文【3】中对Minimax Approximation的定义和Remez 算法，得到在[-5,5]的区间内多项式阶数为1和3时的渐近结果如下图所示。

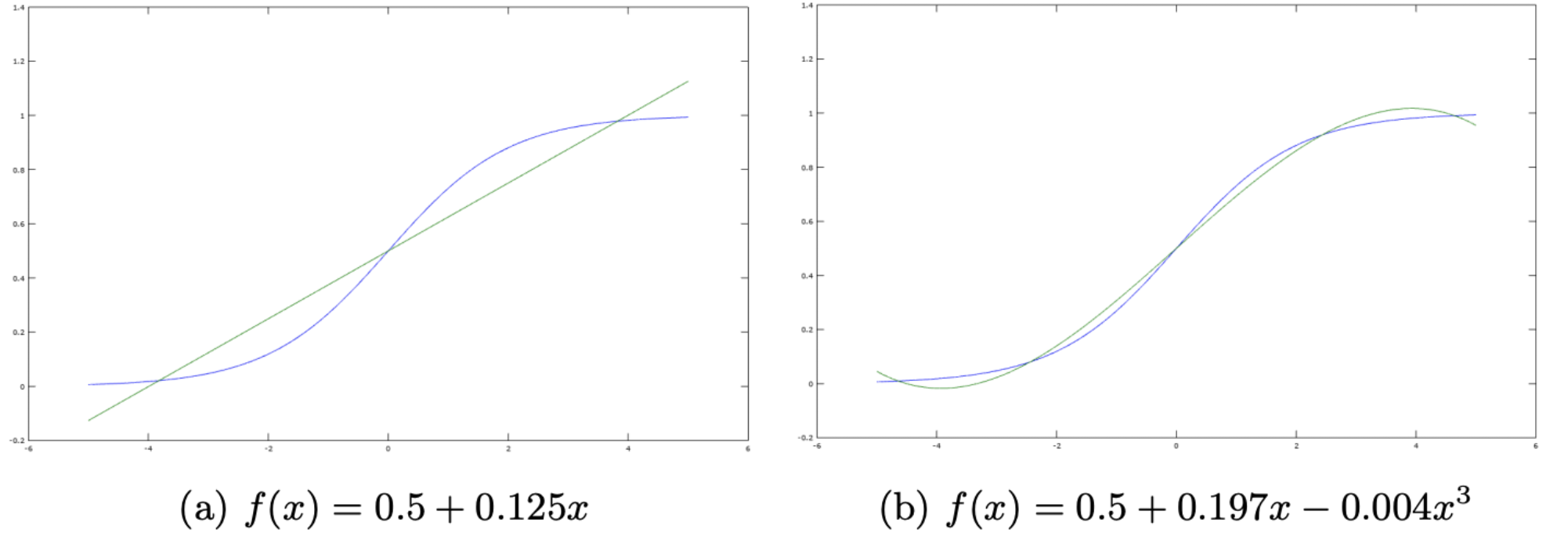
注：在隐语开源代码中，采用了多项式阶数为1的公式。但在论文中，采用了多项式阶数为3的公式。FATE开源代码则使用了Taylor展开【4】。

3 CAESAR：一种安全的可处理大规模稀疏特征的纵向逻辑回归模型

3.1 Motivation

实施安全机器学习模型的两大主要挑战是安全性和高效性。同态加密模型有较好的通讯效率，秘密分享具有可证明的安全性和较好的计算效率，结合两者的优点，本文提出了CAESAR，一种安全的可处理大规模稀疏特征的纵向逻辑回归模型。

3.2 结合HE和SS的安全稀疏矩阵乘法协议

具体的安全稀疏矩阵乘法协议如下：

FATE 给出了一个简洁明了的流程图【5】。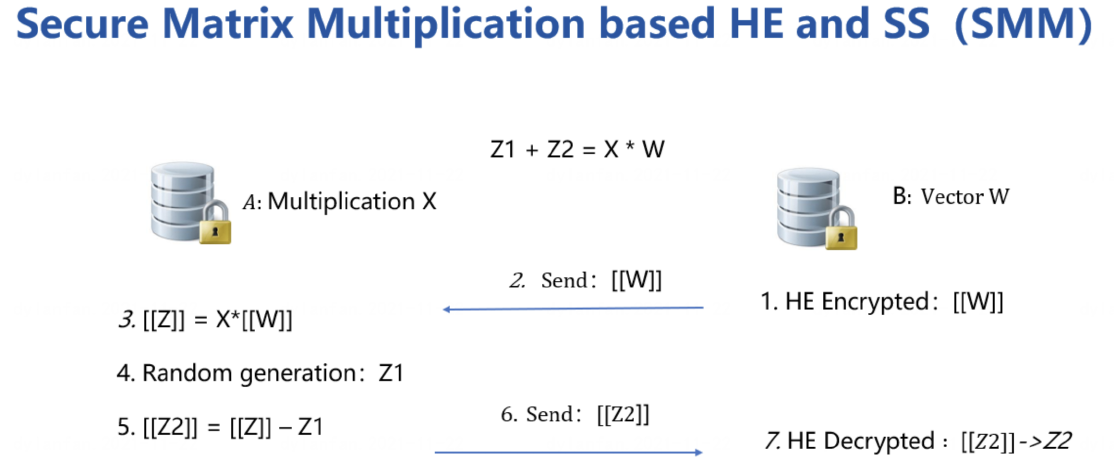

文字版协议流程概括如下：

3.3 安全⼤规模逻辑回归模型

本⽂核⼼安全的可处理⼤规模稀疏特征的逻辑回归算法如下：

FATE 同样给出了一个清晰的流程图【5】。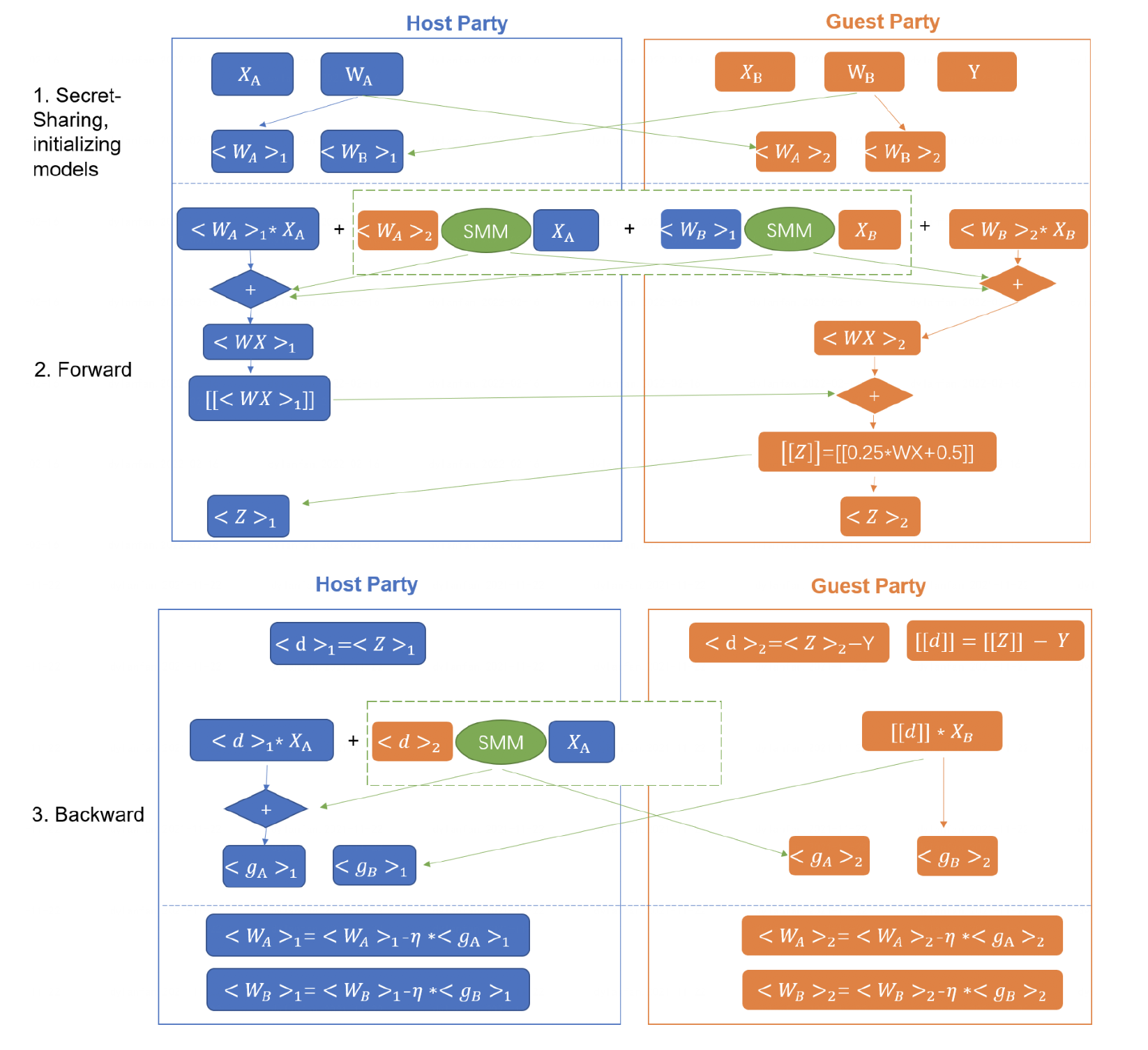

文字版协议流程概括如下：

1. A、B两方初始化模型，交换公钥。
2. 将初始化的权重经过秘密分享，使得两方各有一部分权重的秘密分片。
3. 开始训练模型。在每一次迭代中，A、B两方将己方拥有的部分权重与己方的特征矩阵相乘，再通过3.2的协议计算己方的特征矩阵与对方拥有的部分权重的乘积，A方将得到的结果之和加密发送给B方，B方将自己的到结果与之相加，使用sigmoid近似方法得到逻辑函数的近似值。（注：FATE与隐语使用的近似方法不同，所以在协议中也有所区别）之后，B方将近似值秘密分享给A方。
4. A、B两方计算误差值，由于B方是有标签的一方，可以得到加密后的总误差，计算梯度时可以直接计算再进行秘密分享将部分梯度发送给A方。而A方将己方拥有的部分误差与己方的特征矩阵相乘，再通过3.2的协议计算己方的特征矩阵与对方拥有的部分误差的乘积，A方将最终结果相加得到A方模型的部分梯度。最后，两方更新模型的权重。
5. 模型训练结束后，A、B两方再将拥有的对方模型的部分权重发送给对方，A、B两方最终得到己方的模型。

3.4 CAESAR的优势

在对比A、B两方的通讯复杂度时，CAESAR的通讯复杂度是O(7n+2nd/|B|)，其中 n 是样本量，d 是特征纬度。而目前使用秘密分享的安全协议，如SecureML和ABY，通讯复杂度为O(4nd)。因此，CAESAR协议具有更低的通讯成本，尤其是当数据量很大的时候。

4 协议执行框架

4.1 Motivation

CAESAR协议有较低的通讯复杂度。但由于涉及同态加密运算，计算复杂度会比较高。为了解决计算复杂度的问题，需要设计合理的分布式框架。分析比较了不同的加法同态加密计算，选择了两种加密方式OU和Paillier进行进一步的比较。比较他们的5种计算方法：加密、解密、密文与明文相加、密文与密文相加、密文与明文相乘。经过1000次计算实验，发现OU比Paillier有更好的表现，其中加密是最耗时的步骤。因此，提高加密效率是分布式实施的关键。

4.2 分布式执行框架

分布式执行框架如下图所示：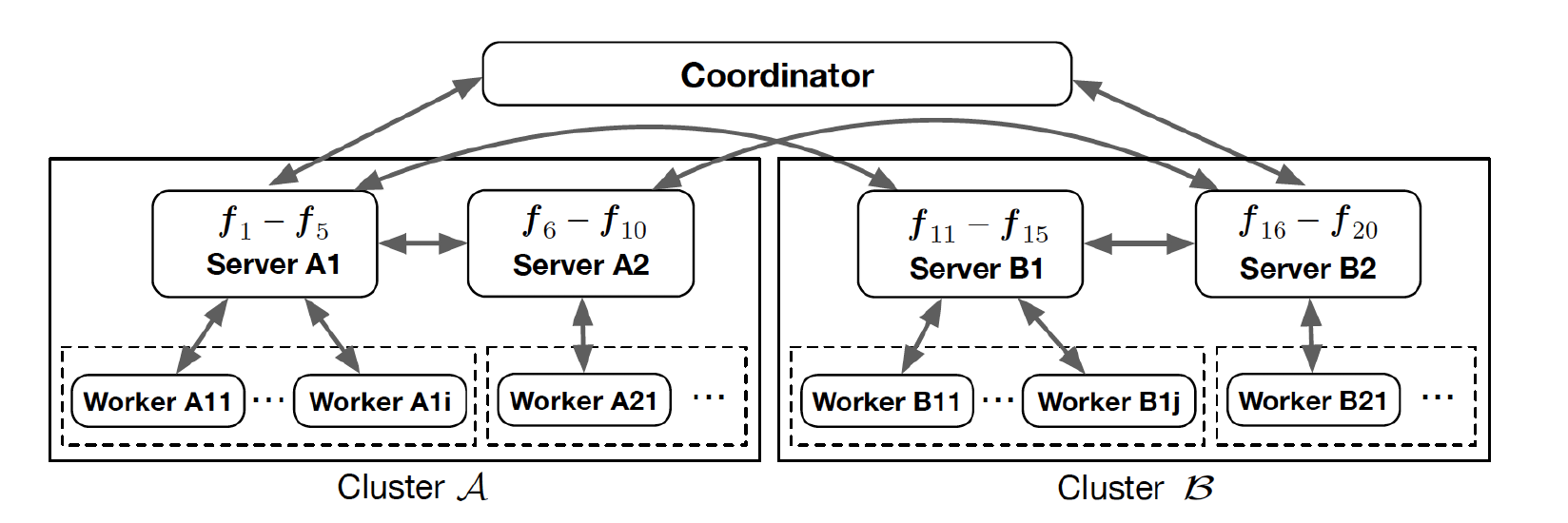

分布式执行框架包含了一个协调者和两个集群，每方各有一个集群。协调者负责控制集群的开始和在某些特定情况中的中止，例如迭代次数。每个集群也是一个分布式学习系统，由服务端和工作节点组成，由参与方各自管理维护。

每个集群有一组服务端将特征和模型纵向切分，如图中每个服务器有5个特征，参与方必须拥有相同数量的服务端，参与两方每一对服务端通过算法学习模型参数。在每个小批次中，所有服务端对先平行计算部分预测值，之后每个集群中的服务端通讯得到所有的预测值。

在运行加密计算时，服务端将明文分发给工作节点进行分布式加密，之后再将加密后的数据发回给相应的服务端进行计算。因为在局域网，集群内部的通讯成本很低。

通过在服务端纵向切分数据和模型，以及将加密运算分配给工作节点，这个执行框架可以处理大数据集。

5 应用与实验结果

5.1 实验设置

场景：互联网金融公司提供线上支付服务，用户通过支付宝进行线上交易支付给商户，控制交易风险对于商户和互联网金融公司都是非常重要的。在这种情况下，互联网金融公司有大量的用户特征和交易特征，商户也有大量的非重复的用户行为特征。而由于数据隔离问题，这些数据没有办法直接明文分享，因此，由于有鲁棒性和解释性的要求，这里运用CAESAR建立一个安全的逻辑回归模型。

数据：本文使用真实的数据集，互联网金融公司拥有30,100个特征，商户拥有70,100个特征，特征稀疏度约0.02%。稀疏特征主要来源于不完整的用户信息或特征工程处理过后的结果。数据集有约123万条数据，包含120万余条正样本和约3万条的负样本。选取发生时间早的80%的交易样本做为训练数据集，发生较晚的20%的交易样本做为测试数据集。

指标：采用四个指标衡量风控模型的表现。包含：AUC、KS、F1、以Recall@0.9precision （当分类模型达到90%精度的recall值）。Recall@0.9precision针对于样本标签不平衡的任务，例如风控。这四个指标值越大，代表模型表现越好。

对比方法：为了测试CAESAR的有效性，将其与仅使用互联网金融公司特征的明文逻辑回归模型、以及现有的基于秘密分享的安全逻辑回归，即SecureML，进行比较。为了测试CAESAR的效率，我们比较它与SecureML。 SecureML基于秘密共享，因此无法处理高维稀疏特征。因为数据是隔离的，所以我们无法在现实中比较CAESAR与使用两方数据的明文逻辑回归的表现。

5.2 对比结果

有效性：下图展示了四个指标的对比结果。SecureML和CAESAR安全逻辑回归模型相对于只使用互联网金融公司特征的明文模型具有更好的表现。CAESAR与SecureML指标一样，说明了CAESAR模型的有效性。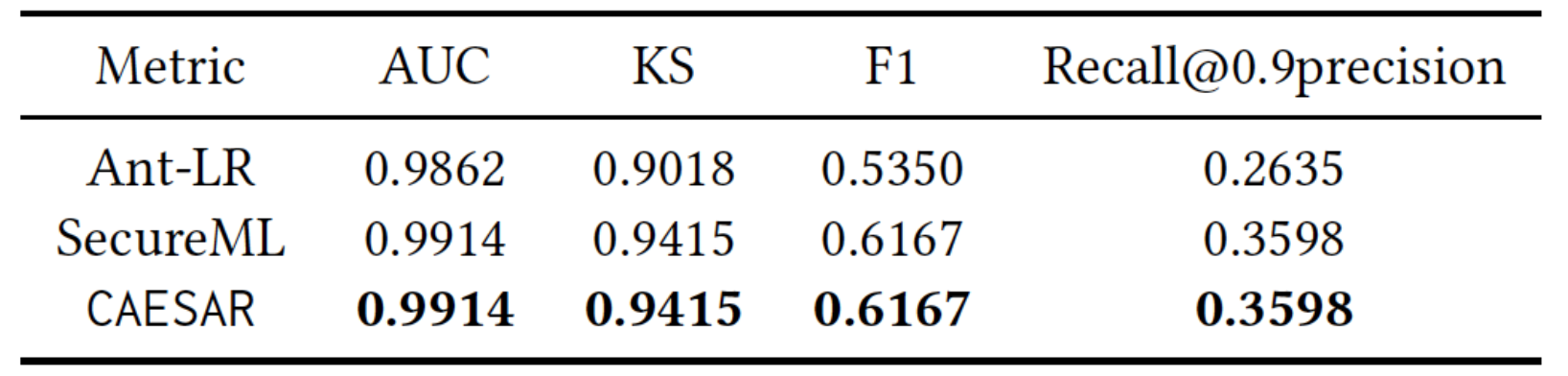

效率：下图展示了当批大小为1024和4096时不同带宽下CAESAR与SecureML在不同样本的运行时间。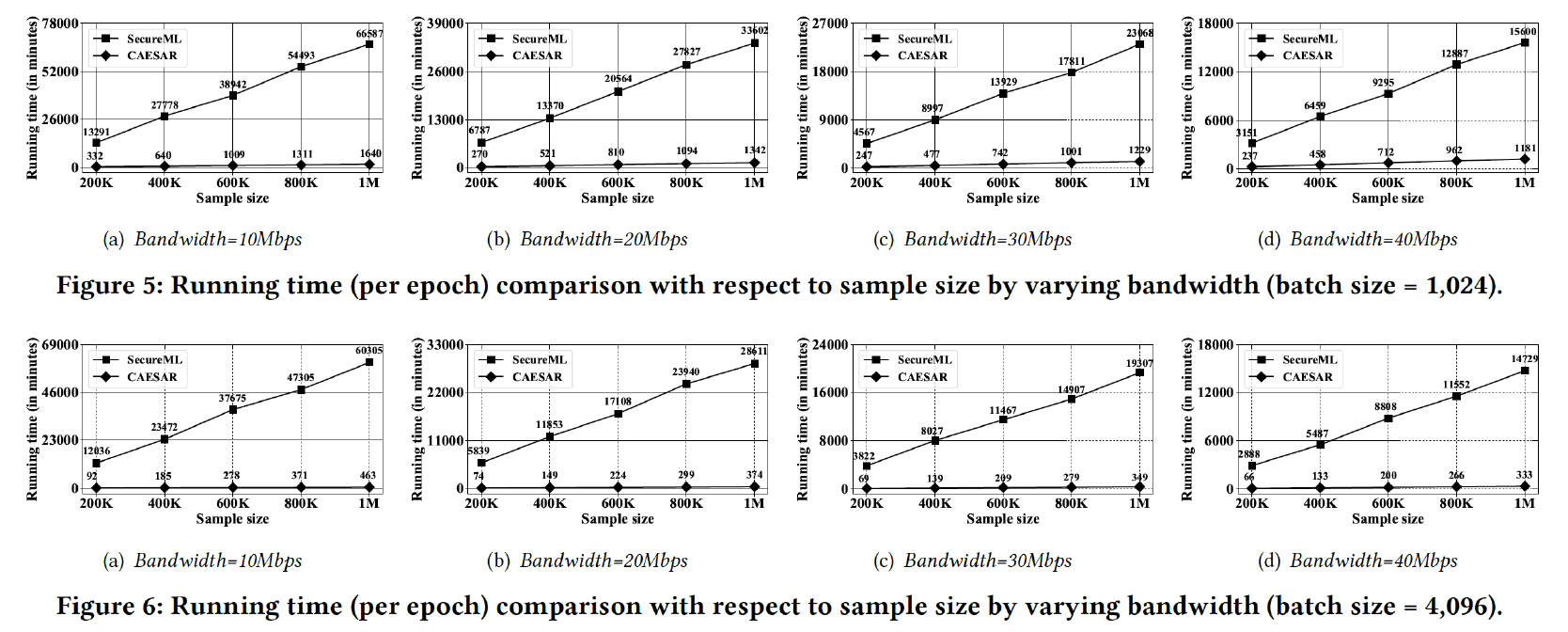

对比CAESAR与SecureML，CAESAR始终比SecureML效率更好。在不同带宽下，CAESAR比SecureML运行速度提高的程度不同，带宽受限时，CAESAR的高效率更加明显。增加批大小，也会使CAESAR的运行效率提高的更加明显。当批大小为4096，带宽为10Mbps时，SecureML的运行时间是CAESAR的130倍。

5.3 参数分析

1. 工作节点的数量对CAESAR的效率有显著的影响。工作节点越多，CAESAR可以处理越大的数据集。
2. CAESAR的运行时间与特征数量呈线性关系。
3. 增加一批次数据量的大小，CAESAR的运行时间会减少。
4. 当带宽变大时，CAESAR的运行时间会减少。当带宽达到一定程度后，运行时间将保持不变。

6 总结

本文为了解决目前安全隐私保护逻辑回归模型的效率和安全问题，提出了CAESAR模型，该模型包含了同态加密与秘密分享技术，保证了安全性的同时提高了效率。将CAESAR模型嵌入分布式框架，在风控场景的实验中，证明了CAESAR模型的效率比之前的SecureML模型更好。

7 与Angel PowerFL的区别分析

以上是对于FATE和隐语开源的基于同态加密与秘密分享技术的纵向LR模型方案论文的翻译总结。另外，Angel PowerFL联邦学习平台也部署了一种安全的纵向联邦LR协议，该协议同样运用了同态加密与秘密分享技术。论文【6】中，先详细的分析了纵向逻辑回归中每种数据的安全性。根据分析完的数据安全性，提出了以下安全纵向LR模型方案。

协议初始化流程图：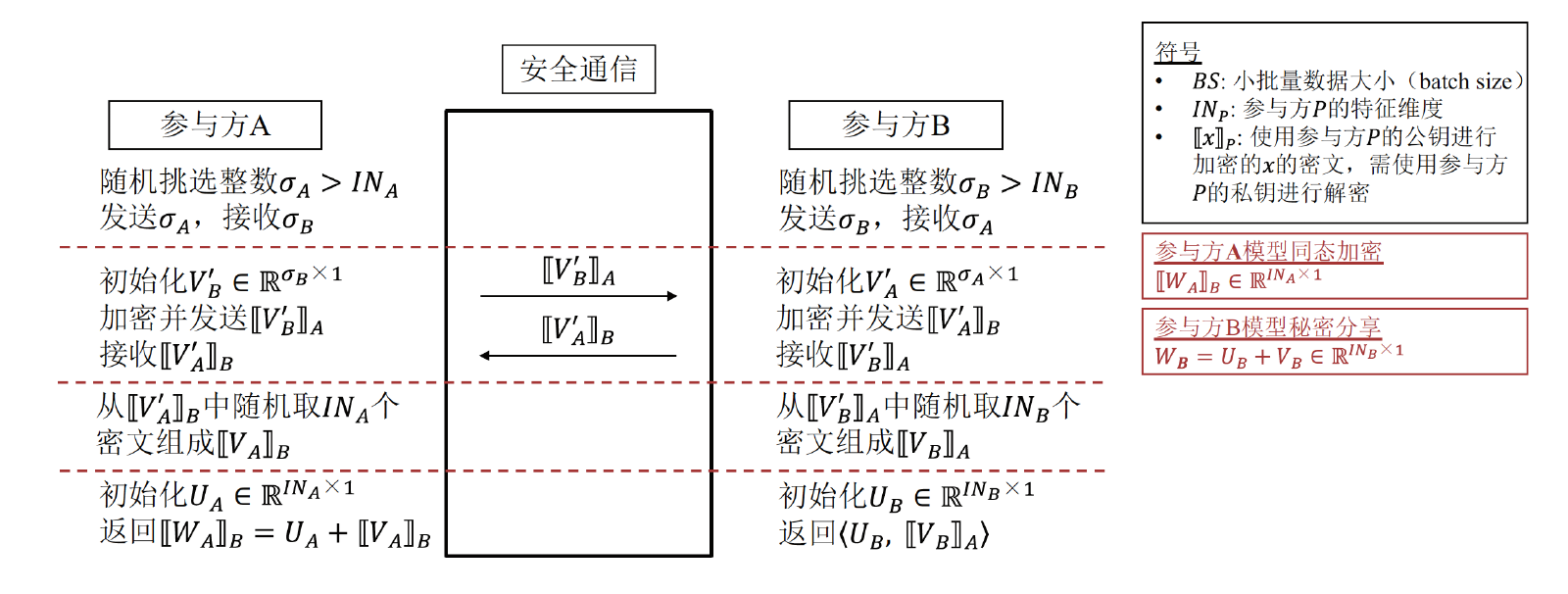

前向计算流程图：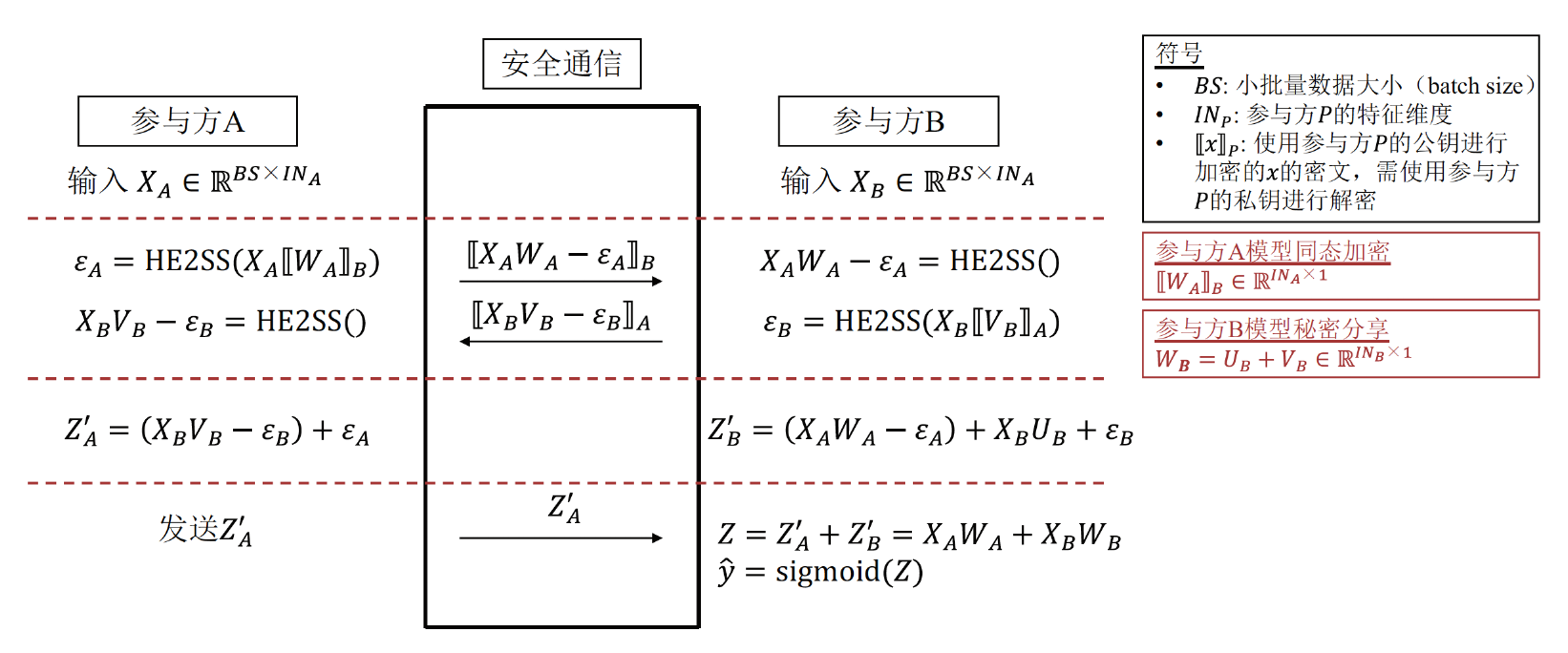

反向计算流程图（模型更新参数）：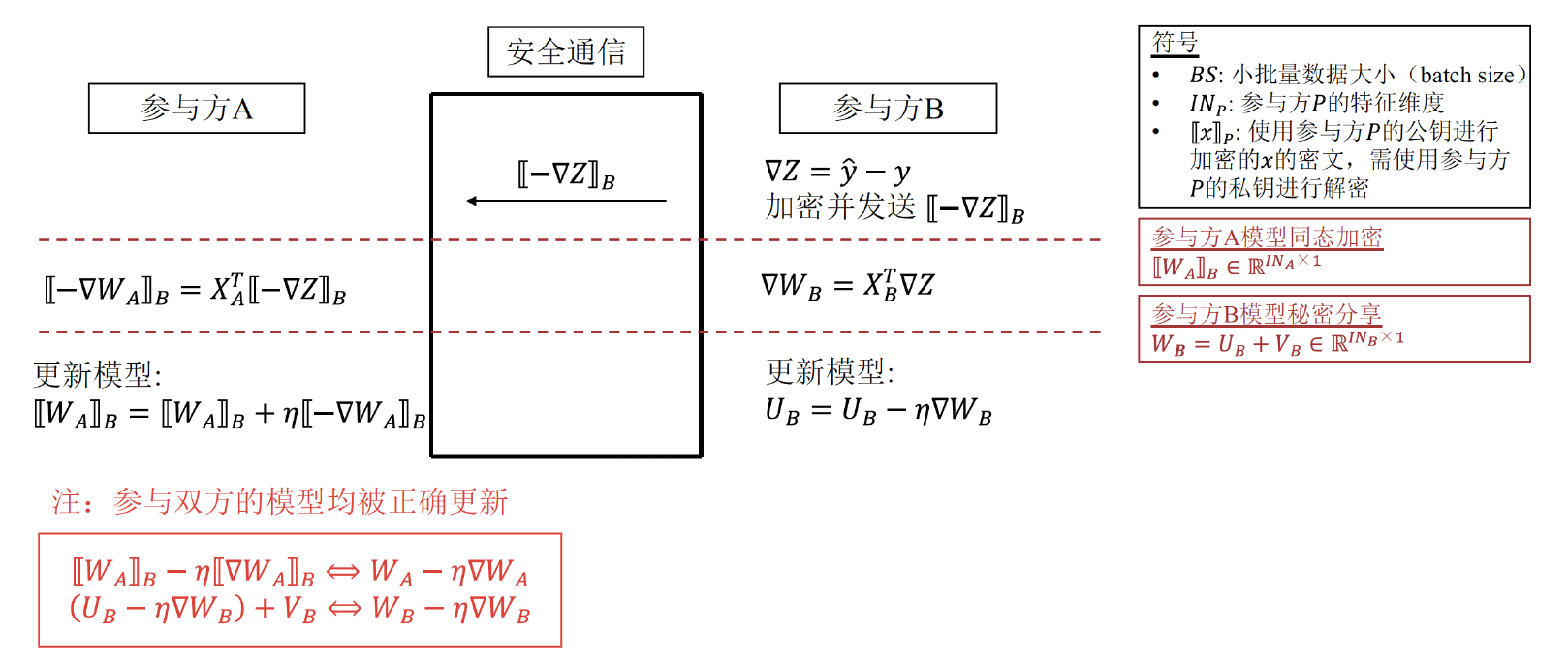

该方案与CAESAR的区别有如下几点：

1. 为了保证参与方无法得知另一参与方的特征维度，在初始化流程阶段，参与双方都随机生成了大于特征维度的整数。为了保护参与方模型权重，对双方的模型权重分别采用了不同的保护方法，参与方A使用了同态加密技术保护模型权重，参与方B使用了秘密分享技术，但是参与方B并没有将权重分享给参与方A，而是都保留在己方。
2. 在前向计算中，A方拥有整体的密文权重，B方持有明文的秘密分片权重和密文的秘密分片权重，A、B两方将己方拥有的密文部分的权重与己方的特征矩阵相乘，再将乘积结果秘密分享给对方，A方将得到的结果之和发送给B方，而B方将自己得到的结果之和加上自己明文的秘密分片权重与特征矩阵的乘积，再加上A方传来的结果得到最终的值，代入到sigmoid函数得到预测值。其中，A方发来的结果非密文形式，所以最终的值也是明文的，因此不需要再对sigmoid函数进行多项式近似计算。
3. 在反向计算中，B方计算明文的反向偏导，然后加密发送给A方，A方计算密文的模型梯度，B方得到明文的模型梯度。参与双方分别进行模型参数更新，其中A方更新全部的模型权重，而B方对模型权重的其中一部分进行更新。
4. CAESAR同态加密方法选择的是OU，而该方案用的是Paillier。

小结：

Angel PowerFL方案相较FATE与Secretflow有两大优点。第一，Angel PowerFL方案计算与通讯开销少，更加简单明了，易于实现。第二，Angel PowerFL方案由于没有对非线性函数使用多项式近似计算，从而保证了联邦逻辑回归模型无损，而FATE与Secretflow都用到了多项式近似计算，对模型的精度略有损失。

然而，到目前为止，FATE、Secretflow、Angel PowerFL均为两方纵向联邦协议。未来可以考虑同态加密结合秘密分享方案能否适用于三方及以上的多方场景、以及其他机器学习模型中。

文献参考

[1] Chaochao Chen, Jun Zhou, Li Wang, Xibin Wu, Wenjing Fang, Jin Tan, Lei Wang, Xiaoxi Ji, Alex Liu, Hao Wang, et al. When homomorphic encryption marries secret sharing: Secure large-scale sparse logistic regression and applications in risk control. arXiv preprint arXiv:2008.08753, 2020.

[2] Mohassel P, Zhang Y. Secureml: A system for scalable privacy-preserving machine learning[C]//2017 IEEE symposium on security and privacy (SP). IEEE, 2017: 19-38.

[3] Chen H, Gilad-Bachrach R, Han K, et al. Logistic regression over encrypted data from fully homomorphic encryption[J]. BMC medical genomics, 2018, 11(4): 3-12.

[4] Hardy S, Henecka W, Ivey-Law H, et al. Private federated learning on vertically partitioned data via entity resolution and additively homomorphic encryption[J]. arXiv preprint arXiv:1711.10677, 2017.

[5]https://github.com/FederatedAI/FATE/blob/3ee02ea81c62d60353b2df40e141529b151d7c67/doc/federatedml_component/logistic_regression.md

[6] 符芳诚, 刘舒, 程勇, 等. 基于同态加密和秘密分享的纵向联邦 LR 协议研究[J]. 信息通信技术与政策, 2022, 48(5): 34.