做一个医学项目,其中在病例评分时会用到单源最短路径的算法。单源最短路径的dijkstra算法的思路如下:
如果存在一条从i到j的最短路径(Vi.....Vk,Vj),Vk是Vj前面的一顶点。那么(Vi...Vk)也必定是从i到k的最短路径。Dijkstra是以最短路径长度递增,逐次生成最短路径的算法。例如:对于源顶点V0,首先选择其直接相邻的顶点中长度最短的顶点Vi,那么当前已知可得从V0到达Vj顶点的最短距离dist[j]=min{dist[j],dist[i]+cost[i][j]}。假设G=<V, E>,源点为V0,U={V0}表示已经标记过的顶点集合,dist[i]记录V0到i的最短距离,cost[i][j]表示边i到j的开销。
1.从V-U中选择使dist[i]值最小的顶点i,将i加入到U中;
2.更新与i直接相邻顶点的dist值。(dist[j]=min{dist[j],dist[i]+cost[i][j]})
3.知道U=V,停止。
利用php特有的性质,其代码如下:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 | function dijkstra(){ $node_info_arr=array( //结点的邻接表结构 array( 'node_id'=>0, //某个结点的id 'next_node'=>array(4,2,1), 'node_type'=>0, 'cost'=>array(10,30,100) ), array( 'node_id'=>4, //某个结点的id 'next_node'=>array(3), 'node_type'=>1, 'cost'=>array(50) ), array( 'node_id'=>3, //某个结点的id 'next_node'=>array(1), 'node_type'=>1, 'cost'=>array(10) ), array( 'node_id'=>2, //某个结点的id 'next_node'=>array(3,1), 'node_type'=>1, 'cost'=>array(60,60) ), array( 'node_id'=>1, //某个结点的id 'next_node'=>array(), 'node_type'=>2, 'cost'=>array() ) ); $start_node_id=false; //起始结点id $i_cost=array(array()); //两个节点之间的开销 $i_dist=array(); //起始点到各点的最短距离 $b_mark=array(); //是否加入了 foreach($node_info_arr as &$node_info){ if($node_info['node_type']==0){ $start_node_id=$node_info['node_id']; //找到初始节点 } foreach($node_info['next_node'] as $key=>$next_node){ $i_cost[$node_info['node_id']][$next_node]=$node_info['cost'][$key]; } $i_dist[$node_info['node_id']]='INF'; //初始化为无穷大 $b_mark[$node_info['node_id']]=false; //初始化未加入 } if($start_node_id===false){ return '302'; } //计算初始结点到各节点的最短路径 $i_dist[$start_node_id]=0; //初始点到其本身的距离为0 $b_mark[$start_node_id]=true; //初始点加入集合 $current_node_id=$start_node_id; //最近加入的节点id $node_count=count($node_info_arr); for($i=0;$i<$node_count;$i++){ $min='INF'; //当前节点的最近距离 if(is_array($i_cost[$current_node_id])){ foreach($i_cost[$current_node_id] as $key=>$val){ if($i_dist[$key]=='INF'||$i_dist[$key]>$i_dist[$current_node_id]+$val){ $i_dist[$key]=$i_dist[$current_node_id]+$val; } } } foreach($i_dist as $key=>$val){ if(!$b_mark[$key]){ if($val!='INF'&&($min=='INF'||$min>$val)){ $min=$val; $candidate_node_id=$key; //候选最近结点id } } } if($min=='INF'){ break; } $current_node_id=$candidate_node_id; $b_mark[$current_node_id]=true; } foreach($i_dist as $key=>$val){ echo $start_node_id.'=>'.$key.':'.$val.'<br />'; }} |
其中例子为图:
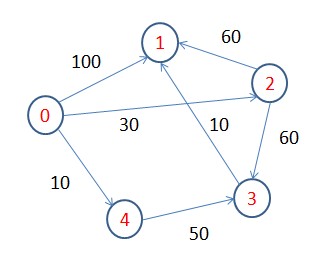
运行结果为:
0=>0:0
0=>4:10
0=>3:60
0=>2:30
0=>1:70











